代数入門問題集
多項式環、体
-
標数
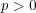 の体
の体
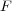 の任意の二元
の任意の二元
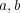 に対して
に対して
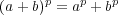 が成り立つことを示せ。
-
が成り立つことを示せ。
-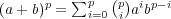 であるが、
であるが、
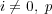 のとき
のとき
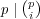 なので主張が成り立つ。
なので主張が成り立つ。
-
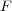 を標数
を標数
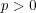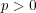 の有限体とする。写像
の有限体とする。写像
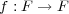 (
(
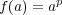 ) は全単射であることを示せ。
-
) は全単射であることを示せ。
-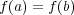 とする。
とする。
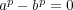 である。
である。
-
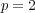 ならば
ならば
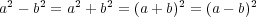 である。
である。
-
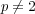 ならば
ならば
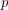 は奇数なので
は奇数なので
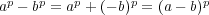 である。
である。
よっていずれの場合も
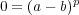 となる。
となる。
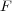 は体なので
は体なので
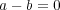 、すなわち
、すなわち
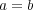 となる。よって
となる。よって
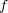 は単 射である。
は単 射である。
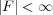 なので
なので
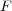 から
から
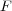 への単射
への単射
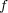 は全単射である。
は全単射である。
-
-
元数が
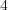 の有限体
の有限体
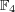 を構成し、その加法と乗法に関する演算表を書け。
-
を構成し、その加法と乗法に関する演算表を書け。
-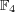 は
は
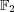 上
上
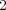 次元ベクトル空間の構造をもつので、その基底を
次元ベクトル空間の構造をもつので、その基底を
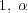 とする。このとき
とする。このとき
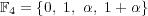 である。また
である。また
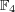 の乗法群
の乗法群
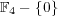 は位数
は位数
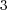 の群になるので、それは巡回群である。以上より、以下の演算表を得る。
の群になるので、それは巡回群である。以上より、以下の演算表を得る。
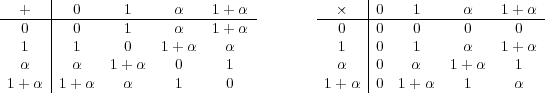
(一般に有限体
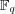 の乗法群
の乗法群
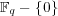 は素数位数でなくても巡回群になる。)
は素数位数でなくても巡回群になる。)
-
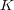 を体とし
を体とし
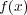 (
(
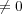 ) を
) を
 次の
次の
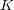 係数多項式とする。このとき
係数多項式とする。このとき
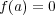 となる
となる
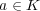 は高々
は高々
 個 であることを示せ。 (
個 であることを示せ。 (
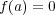 となる
となる
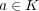 を
を
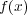 の根という。)
-次数に関する帰納法で示す。次数が
の根という。)
-次数に関する帰納法で示す。次数が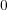 すなわち
すなわち
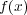 が
が
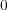 でない定数ならば根はないので、主張は正しい。
でない定数ならば根はないので、主張は正しい。
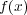 を
を
 次 以上の次数の多項式とする。
次 以上の次数の多項式とする。
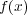 が根・もたなければ主張は成り立つので、
が根・もたなければ主張は成り立つので、
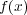 は根
は根
 をもつとする。因数定理により
をもつとする。因数定理により
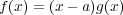 と書けて
と書けて
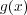 の次数は
の次数は
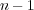 である。
である。
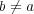 がやはり
がやはり
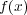 の根であるとすると、
の根であるとすると、
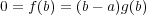 である。
である。
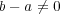 と
と
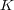 が体、よって整域であることにより
が体、よって整域であることにより
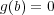 である。したがって
である。したがって
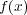 の根は
の根は
 であるか、または
であるか、または
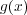 の根である。帰納法の仮定により
の根である。帰納法の仮定により
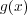 の根は高々
の根は高々
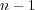 個なので、
個なので、
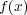 の根は高々
の根は高々
 個である。
個である。
(
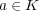 が多項式
が多項式
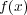 の根であることと
の根であることと
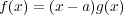 となる多項式
となる多項式
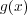 が存在することは同値である。これを因数定理という。)
が存在することは同値である。これを因数定理という。)
-
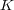 を体とし、
を体とし、
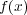 を
を
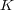 係数多項式とする。
係数多項式とする。
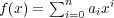 に対して
に対して
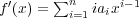 とおいて、これを
とおいて、これを
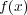 の形式的な微分という。
の形式的な微分という。
- (1) 多項式の形式的な微分についても、積の微分に関する公式
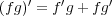 は成り立つことを示せ。
は成り立つことを示せ。
- (2)
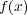 が重根
が重根
 をもつことと
をもつことと
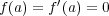 となることが同値であることを示せ。ただし
となることが同値であることを示せ。ただし
 が
が
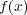 の 重根であるとは、多項式
の 重根であるとは、多項式
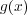 が存在して
が存在して
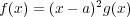 と書けることとする。
と書けることとする。
-- (1) 形式的な微分が和とスカラー倍を保つこと、すなわち
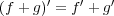 ,
,
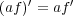 (
(
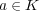 ) となること、は計算によってすぐに確かめることができる。
) となること、は計算によってすぐに確かめることができる。
単項式の積
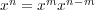 に つ い て 示 す。
に つ い て 示 す。
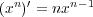 であり、また
であり、また
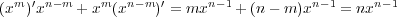 なので、この場合 には
なので、この場合 には
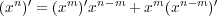 は成り立つ。
は成り立つ。
一般の場合を考える。
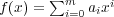 ,
,
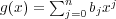 とする。
が成り立つ。
とする。
が成り立つ。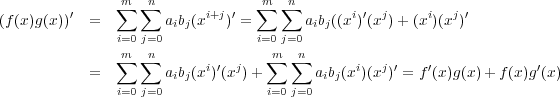
- (2)
 が
が
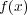 の重根であるとすると
の重根であるとすると
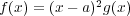 と書ける。このとき
と書ける。このとき
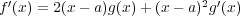 なので
なので
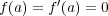 である。
である。
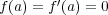 と仮定する。因数定理より
と仮定する。因数定理より
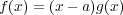 と書ける。
と書ける。
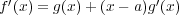 より
より
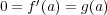 である。よって因数定理より
である。よって因数定理より
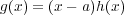 と書くことができ、
と書くことができ、
 は
は
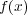 の重根である。
の重根である。
- (1) 多項式の形式的な微分についても、積の微分に関する公式
-
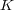 を体とする。写像
を体とする。写像
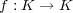 が多項式写像であるとは、ある
が多項式写像であるとは、ある
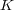 係数多項式
係数多項式
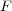 が存在して、任意の
が存在して、任意の
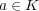 に対して
に対して
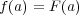 となることとする。
となることとする。
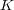 が有限体であるとき、任意の写像
が有限体であるとき、任意の写像
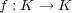 は多項式写像であることを示せ。
-
は多項式写像であることを示せ。
-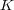 の元数を
の元数を
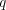 とする。
とする。
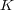 から
から
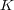 への写像は
への写像は
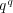 個ある。一方で、
個ある。一方で、
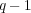 次以下の多項式も
次以下の多項式も
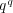 個あるので、これらがすべて写像として異なることをいえばよい。
個あるので、これらがすべて写像として異なることをいえばよい。
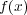 ,
,
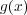 を
を
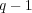 次以下の多項式とし、
次以下の多項式とし、
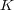 から
から
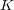 への写像として等しいと仮定する。このとき
への写像として等しいと仮定する。このとき
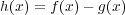 も
も
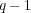 次以下の多項式であって、
次以下の多項式であって、
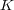 の任意の元が
の任意の元が
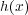 の根になる。
の根になる。
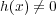 ならば、問
4 によっ てその根の数は高々
ならば、問
4 によっ てその根の数は高々
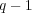 個であり、これは矛盾である。よって
個であり、これは矛盾である。よって
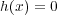 、すなわち
、すなわち
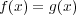 となる。
となる。
(多項式
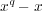 は
は
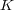 のすべての元を根にもち、写像としては
のすべての元を根にもち、写像としては
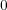 と等しくなる。)
と等しくなる。)
-
体
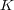 上の二つの多項式で、多項式としては異なり、等しい多項式写像を定めるものを具体的に一つ答えよ。
-
上の二つの多項式で、多項式としては異なり、等しい多項式写像を定めるものを具体的に一つ答えよ。
- -
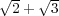 を根にもつ次数最小で最高次係数が
を根にもつ次数最小で最高次係数が
 の有理数係数多項式を求めよ。
-
の有理数係数多項式を求めよ。
-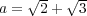 とおく。
で ある。ここで
とおく。
で ある。ここで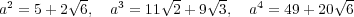
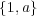 ,
,
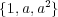 ,
,
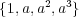 はいずれも
はいずれも
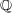 上一次独立であることが簡単に分かり、したがって
上一次独立であることが簡単に分かり、したがって
 は
は
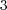 次以下の多項式の根にはならない。
次以下の多項式の根にはならない。
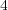 次式については
次式については
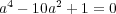 が成り立つことが分かるので、求める多項式は
が成り立つことが分かるので、求める多項式は
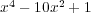 である。
である。
(
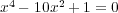 の根は
の根は
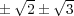 である。)
である。)
-
![√ - √ -ℚ [ 2] = {a+ b 2 | a,b ∈ ℚ }](img/algex621x.gif) とおく。
とおく。
![√-ℚ[ 2]](img/algex622x.gif) は通常の演算で体であることを示せ。
-
は通常の演算で体であることを示せ。
-![ℚ [√2 ]](img/algex2115x.gif) が通常の和、差、積で閉じていること、すなわち
が通常の和、差、積で閉じていること、すなわち
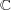 の部分環であることは明らかである。したがって
の部分環であることは明らかである。したがって
![0 ⁄= x = a +b√2-∈ ℚ [√2-]](img/algex2117x.gif) が逆元をもつことを示せばよい。もちろん
が逆元をもつことを示せばよい。もちろん
 は
は
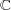 では逆元をもち、それは
である。よって
では逆元をもち、それは
である。よって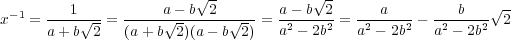
 も
も
![ℚ[√2]](img/algex2122x.gif) の元であり、したがって
の元であり、したがって
![ℚ [√2-]](img/algex2123x.gif) は体である。
は体である。
(同様にして、一般に
![ℚ [√m--] = {a+ b√m | a,b ∈ ℚ}](img/algex2124x.gif) (
(
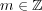 ) も体であることが分かる。)
) も体であることが分かる。)
-
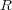 を整域とし
を整域とし
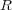 の部分集合
の部分集合
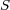 は
は
-
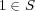 ,
,
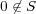
-
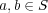 ならば
ならば
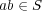
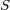 を
を
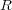 の積閉集合という。直積集合
の積閉集合という。直積集合
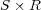 に
に
 のときに
のときに
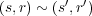 として 関係
として 関係
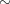 を定める。
を定める。
- (1)
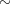 は同値関係であることを示せ。
は同値関係であることを示せ。
- (2)
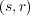 を含む
を含む
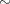 による同値類を
による同値類を
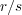 と書くことにする。また同値類全体の集合を
と書くことにする。また同値類全体の集合を
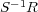 と書く。
と書く。
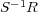 に加法と乗法を
によって定めることができることを示せ。
に加法と乗法を
によって定めることができることを示せ。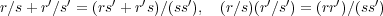
- (3) 上の演算が、加法に関する交換法則、結合法則、乗法に関する結合法則、分配法則を満たすことを示せ。
- (4) 以上より
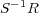 は環の構造をもつ。これを
は環の構造をもつ。これを
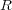 の
の
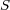 による商環という。特に
による商環という。特に
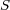 として
として
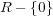 をとれば、 これは積閉集合である。このときの商環
をとれば、 これは積閉集合である。このときの商環
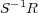 は体であることを示せ。 (この体を整域
は体であることを示せ。 (この体を整域
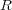 の商体という。)
の商体という。)
- (5)
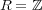 のとき、その商体は何かを考えよ。
のとき、その商体は何かを考えよ。
-- (1) 対称律、反射律は明らかである。推移律を示す。
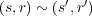 かつ
かつ
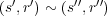 と仮定する。このとき
と仮定する。このとき
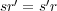 ,
,
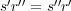 である。したがって
である。したがって
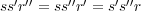 である。ここで
である。ここで
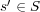 より
より
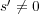 で、 かつ
で、 かつ
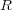 が整域なので
が整域なので
 となる。よって
となる。よって
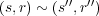 が成り立つ。
が成り立つ。
- (2)
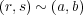 ,
,
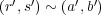 と仮定する。仮定より
と仮定する。仮定より
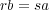 ,
,
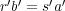 が成り立っている。したがって
となり
が成り立っている。したがって
となり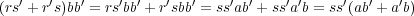
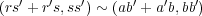 が成り立つ。よって和は矛盾なく定義される。また
が成り立つ。よって和は矛盾なく定義される。また
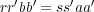 よ り
よ り
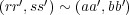 であり、積も矛盾なく定義される。
であり、積も矛盾なく定義される。
- (3)
- [加法に関する交換法則、結合法則]加法についての交換法則が成り立つことはすぐに分かる。
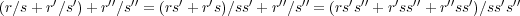 であ り
であ り
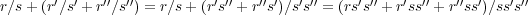 であるから結合法則 は成り立つ。
であるから結合法則 は成り立つ。
- [乗法に関する結合法則]
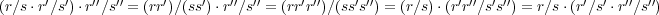 で あるから結合法則は成り立つ。
で あるから結合法則は成り立つ。
- [分配法則]
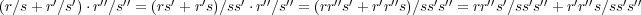 こ こ で
こ こ で
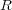 が整域で
が整域で
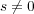 ,
,
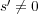 であるから
であるから
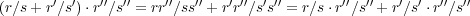 となる。
となる。
- [加法に関する交換法則、結合法則]加法についての交換法則が成り立つことはすぐに分かる。
- (4)
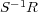 の零元は
の零元は
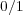 であり、単位元は
であり、単位元は
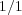 であることに注意しておく。
であることに注意しておく。
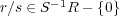 とすると
とすると
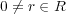 ,
,
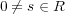 である。よって
である。よって
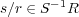 となり
となり
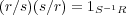 となる。したがって
となる。したがって
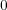 でない任意の元が正則元となり
でない任意の元が正則元となり
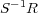 は体である。
は体である。
- (5)
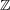 の商体は有理数体
の商体は有理数体
 である。
である。
-
-
- (1) 整域
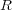 上の一変数多項式環
上の一変数多項式環
![R[x]](img/algex652x.gif) はまた整域であることを示せ。
はまた整域であることを示せ。
- (2) 整域
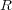 上の
上の
 変数多項式環
変数多項式環
![R[x1,x2,⋅⋅⋅ ,xn]](img/algex655x.gif) は整域であることを示せ。
は整域であることを示せ。
-- (1)
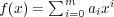 ,
,
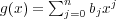 とし、
とし、
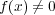 ,
,
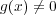 と仮定する。係数が
と仮定する。係数が
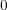 である項を略 して
である項を略 して
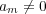 ,
,
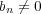 と仮定してよい。このとき
と仮定してよい。このとき
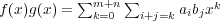 であり、特に
であり、特に
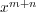 の係数は
の係数は
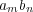 である。
である。
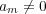 ,
,
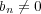 で
で
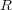 が整域であることにより
が整域であることにより
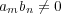 である。よって
である。よって
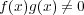 である。
である。
- (2)
 に関する帰納法で示す。
に関する帰納法で示す。
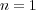 のときは (1) である。
のときは (1) である。
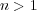 とする。
とする。
![R [x1,x2,⋅⋅⋅ ,xn]](img/algex2182x.gif) は
は
![R [x1,x2,⋅⋅⋅ ,xn -1]](img/algex2183x.gif) 上一変数多項式環
上一変数多項式環
![R [x1,x2,⋅⋅⋅ ,xn-1][xn]](img/algex2184x.gif) と見ることができる。帰納法の仮定から
と見ることができる。帰納法の仮定から
![R [x1,x2,⋅⋅⋅ ,xn -1]](img/algex2185x.gif) は整域であるから (5) より
は整域であるから (5) より
![R[x1,x2,⋅⋅⋅ ,xn]](img/algex2186x.gif) も整域である。
も整域である。
- (1) 整域
-
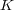 を体とする。
を体とする。
- (1)
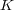 上の一変数多項式環
上の一変数多項式環
![K [x ]](img/algex658x.gif) は単項イデアル整域 (§3 問
17 参照) であることを示せ。
は単項イデアル整域 (§3 問
17 参照) であることを示せ。
- (2)
![f(x),g(x ) ∈ K[x]](img/algex659x.gif) に対して
に対して
![(f (x),g(x)) = {f(x)a(x)+ g(x)b(x ) | a(x),b(x) ∈ K [x]}](img/algex660x.gif) とおくと、
とおくと、
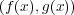 は
は
![K [x]](img/algex662x.gif) のイデアルであることを示せ。
のイデアルであることを示せ。
- (3) (1), (2) より、
![f(x),g(x) ∈ K [x]- {0}](img/algex663x.gif) に対して
に対して
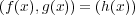 となる
となる
![h(x) ∈ K [x]](img/algex665x.gif) が存在する。最高次係数で割って
が存在する。最高次係数で割って
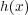 の最高次係数は
の最高次係数は
 であると仮定してよい。このとき
であると仮定してよい。このとき
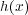 を
を
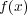 と
と
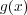 の最大公約元といい、
の最大公約元といい、
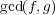 と書くことにする。
と書くことにする。
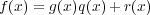 ,
,
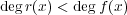 とするとき
とするとき
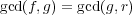 であることを示せ。
であることを示せ。
-- (1)
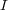 を
を
![K [x]](img/algex2188x.gif) の
の
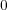 でないイデアルとする。
でないイデアルとする。
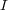 の
の
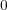 でない元で、次数最小のものを
でない元で、次数最小のものを
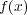 とする。 (
とする。 (
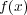 は 一意的ではないが、その一つをとり固定する。)
は 一意的ではないが、その一つをとり固定する。)
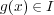 とする。多項式の割り算を考えれば
となる
とする。多項式の割り算を考えれば
となる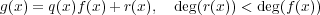
![q(x), r(x) ∈ K [x]](img/algex2196x.gif) が存在する。ここで
が存在する。ここで
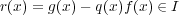 となるので、
となるので、
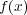 の次数の 最小性から
の次数の 最小性から
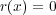 である。したがって
である。したがって
![g(x) ∈ f (x)K [x ]](img/algex2200x.gif) である。よって
である。よって
![I ⊂ f(x)K [x]](img/algex2201x.gif) となる。一方で
となる。一方で
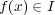 なので
なので
![f(x)K[x] ⊂ I](img/algex2203x.gif) は明らかに成り立ち
は明らかに成り立ち
![I = f(x)K [x]](img/algex2204x.gif) となる。したがって
となる。したがって
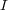 は単項イデアルで ある。
は単項イデアルで ある。
問11 より
![K [x]](img/algex2206x.gif) は整域なので
は整域なので
![K [x ]](img/algex2207x.gif) は単項イデアル整域である。
は単項イデアル整域である。
- (2)
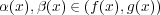 ,
,
![h(x) ∈ K [x]](img/algex2209x.gif) とする。
とする。
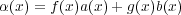 ,
,
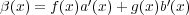 となる
となる
![a(x), a′(x), b(x ), b′(x) ∈ K [x]](img/algex2212x.gif) が存在する。このとき
であるから
が存在する。このとき
であるから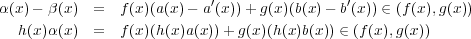
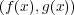 は
は
![K [x]](img/algex2215x.gif) のイデアルである。
のイデアルである。
- (3) (1) よりイデアルの次数最小の元はスカラー倍を除いて一意的に定まるので
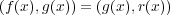 を示せば十分であ る。
を示せば十分であ る。
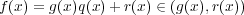 ,
,
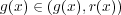 であるから
であるから
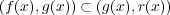 が成り立つ。 また
が成り立つ。 また
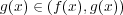 ,
,
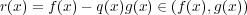 より
より
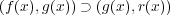 が成り立つ。よって
が成り立つ。よって
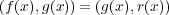 である。
である。
- (1)
-
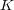 を体とする。
を体とする。
![f(x) ∈ K [x]](img/algex676x.gif) を既約な多項式とする。このとき
を既約な多項式とする。このとき
![K [x]∕(f(x))](img/algex677x.gif) は体であることを示せ。
-
は体であることを示せ。
- -
![ℚ [x]∕(x2 - 2)](img/algex678x.gif) は本質的に
は本質的に
![√ -ℚ[ 2]](img/algex679x.gif) (問
9
参照) と同じ体であることを示せ。 (本質的に同じ体であるとは、集合とし ての全単射で、和と積を保つものが存在することをいうこととする。このとき二つの体は同型であるという。)
-自然な全射
(問
9
参照) と同じ体であることを示せ。 (本質的に同じ体であるとは、集合とし ての全単射で、和と積を保つものが存在することをいうこととする。このとき二つの体は同型であるという。)
-自然な全射![ℚ[x] → ℚ[x]∕(x2 - 2)](img/algex2239x.gif) による
による
![f(x ) ∈ ℚ[x]](img/algex2240x.gif) の像を
の像を
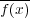 と書くことにする。
と書くことにする。
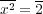 に注意すれば、任意の
に注意すれば、任意の
![f(x) ∈ ℚ [x]](img/algex2243x.gif) は
は
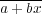 (
(
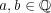 ) と一意的に表されることが分かる。このとき
) と一意的に表されることが分かる。このとき
![Γ : ℚ [x]∕(x2 - 2) → ℚ[√2]](img/algex2246x.gif) を
を
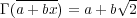 と定めれば、これは全単射である。
と定めれば、これは全単射である。
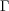 が和を保存することはすぐに分かる。また
となり、積を保存することも分かる。
が和を保存することはすぐに分かる。また
となり、積を保存することも分かる。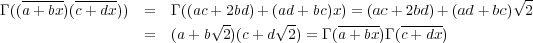
-
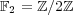 (元数
(元数
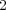 の有限体) とする。
の有限体) とする。
- (1)
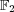 上の既約な
上の既約な
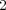 次多項式
次多項式
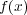 を見付けよ。
を見付けよ。
- (2)
![F2[x]∕(f(x))](img/algex685x.gif) は本質的に問
3 の体
は本質的に問
3 の体
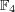 と同じ体であることを示せ。
と同じ体であることを示せ。
- - (1)
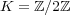 とする。このとき
とする。このとき
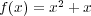 は多項式としては
は多項式としては
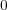 ではないが
ではないが
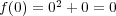 ,
,
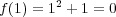 であり、
であり、
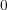 と同じ多項式写像を与える。
と同じ多項式写像を与える。
![g(x) ∈ K[x]](img/algex2224x.gif) に対して
に対して
![g(x)+ (f(x)) ∈ K [x]∕(f (x))](img/algex2225x.gif) を
を
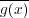 と書くことにする。
と書くことにする。
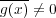 、すなわち
、すなわち
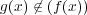 とする。このとき
とする。このとき
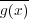 が逆元をもつことを示せばよい。
が逆元をもつことを示せばよい。
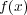 を割り切る多項式は
を割り切る多項式は
 と
と
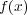 自身しかないので、問
自身しかないので、問
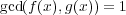 である。よって、やはり問
である。よって、やはり問
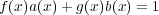 となる
となる
![a(x),b(x) ∈ K [x]](img/algex2235x.gif) が存在する。このとき
が存在する。このとき
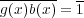 となり、
となり、
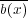 が
が
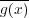 の逆元である。
の逆元である。
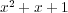 は既約である。 (既約でないならば
は既約である。 (既約でないならば
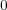 または
または
 を根にもたなくてはならない。)
を根にもたなくてはならない。)
![- - -------F2[x]∕(f(x)) = {0,1, x,1 + x}](img/algex2253x.gif) である。加法、乗法の演算表を書けば問
である。加法、乗法の演算表を書けば問
 は
は
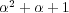 を満たしている。)
を満たしている。)