代数入門問題集
二項演算、半群、モノイド
-
集合
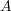 の二項演算の定義を答えよ。
-
の二項演算の定義を答えよ。
-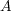 の二項演算とは、写像
の二項演算とは、写像
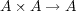 のことである。
のことである。
-
集合
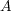 がちょうど二つの要素をもつとする。
がちょうど二つの要素をもつとする。
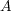 の二項演算はいくつあるか。
-一般に、有限集合
の二項演算はいくつあるか。
-一般に、有限集合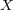 ,
,
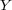 について
について
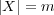 ,
,
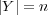 とすると、
とすると、
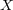 から
から
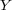 への写像は
への写像は
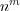 個ある。
個ある。
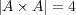 ,
,
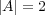 であるから、二項演算は
であるから、二項演算は
 個ある。
個ある。
-
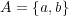 を
を
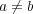 なる集合とする。
なる集合とする。
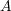 の二項演算で、結合法則をみたすものを具体的に一つ構成せよ。
-例えば以下のようなものがある。
の二項演算で、結合法則をみたすものを具体的に一つ構成せよ。
-例えば以下のようなものがある。- (1) 任意の
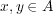 に対して
に対して
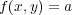 であるもの。
であるもの。
- (2)
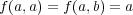 ,
,
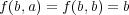 で定まるもの。
で定まるもの。
- (3)
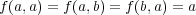 ,
,
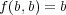 で定まるもの。
で定まるもの。
- (4)
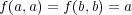 ,
,
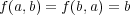 で定まるもの。
で定まるもの。
- (1) 任意の
-
以下のものは、半群、モノイド、群、そのいずれでもないか、最も適当なものをそれぞれ答えよ。
- (1) 集合
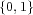 で通常の加法を演算とするもの。
で通常の加法を演算とするもの。
- (2) 集合
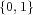 で通常の乗法を演算とするもの。
で通常の乗法を演算とするもの。
- (3) 集合
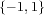 で通常の乗法を演算とするもの。
で通常の乗法を演算とするもの。
- (4) 集合
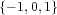 で通常の乗法を演算とするもの。
で通常の乗法を演算とするもの。
- (5) 実数を成分とする
 次正方行列の全体で通常の加法を演算とするもの。
次正方行列の全体で通常の加法を演算とするもの。
- (6) 実数を成分とする
 次正方行列の全体で通常の乗法を演算とするもの。
次正方行列の全体で通常の乗法を演算とするもの。
- (7) 実数を成分とする
 次正則行列の全体で通常の乗法を演算とするもの。
次正則行列の全体で通常の乗法を演算とするもの。
-(1) いずれでもない (2) モノイド (3) 群 (4) モノイド (5) 群 (6) モノイド (7) 群 - (1) 集合
-
実数を成分とする
 次正方行列
次正方行列
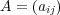 ,
,
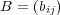 ,
,
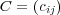 について
について
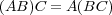 が成り立つことを示せ。
-
が成り立つことを示せ。
- の
の
 - 成分は
- 成分は
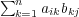 である。
である。
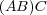 ,
,
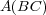 の
の
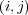 - 成分はそれぞれ
であるから、これらは等しい。
- 成分はそれぞれ
であるから、これらは等しい。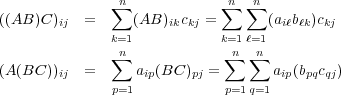
(二つの行列が等しいことの定義は、すべての対応する成分が等しいことである。)
-
複素数
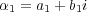 ,
,
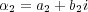 ,
,
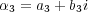 について
について
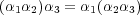 が成り立つことを示せ。 ただし
が成り立つことを示せ。 ただし
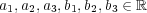 で
で
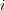 は虚数単位とする。
-となるから、この二つの値は等しい。
は虚数単位とする。
-となるから、この二つの値は等しい。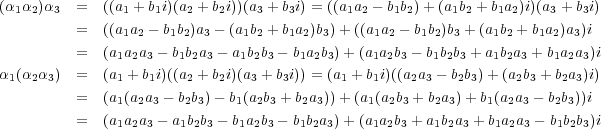
-
直積集合
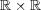 に
で 二項演算を定める。
に
で 二項演算を定める。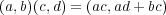
- (1) これが結合法則を満たすことを示せ。 (よってこれは半群である。)
- (2) 単位元を求めよ。 (よってこれはモノイドである。)
- (3) 正則元を決定し、その逆元も求めよ。
-- (1)
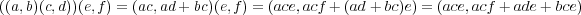 である。また
である。また
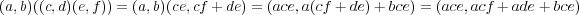 であ る。よって
であ る。よって
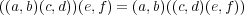 であり、結合法則が成り立つ。
であり、結合法則が成り立つ。
- (2)
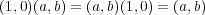 となるので
となるので
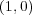 が単位元である。
が単位元である。
- (3)
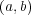 について、
について、
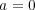 ならば
ならば
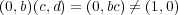 であるから
であるから
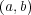 は正則元ではない。
は正則元ではない。
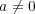 とする。このとき
とする。このとき
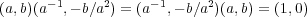 が成り立つ。よって
が成り立つ。よって
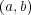 が正則元となる ための必要十分条件は
が正則元となる ための必要十分条件は
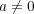 で、そのときの逆元は
で、そのときの逆元は
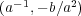 である。
である。
-
直積集合
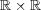 に
で 二項演算を定める。
に
で 二項演算を定める。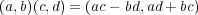
- (1) これが結合法則を満たすことを示せ。
- (2) 単位元を求めよ。
- (3) 正則元を決定し、その逆元も求めよ。
-- (1) 省略。
(
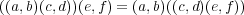 を計算によって確かめればよい。実は問
6
と本質的に同じであ る。)
を計算によって確かめればよい。実は問
6
と本質的に同じであ る。)
- (2)
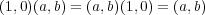 となるので
となるので
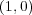 が単位元である。
が単位元である。
- (3)
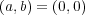 は零元なので正則元ではない。
は零元なので正則元ではない。
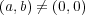 と仮定する。
と仮定する。
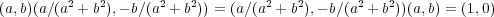 が成り立つ。よって
が成り立つ。よって
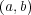 が正則元 となるための必要十分条件は
が正則元 となるための必要十分条件は
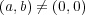 で、そのときの逆元は
で、そのときの逆元は
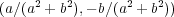 であ る。
であ る。
- 直積集合
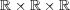 に
で和と積を定める。
に
で和と積を定める。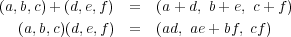
- (1) 積が結合法則を満たすことを示せ。
- (2) 積に関する単位元を求めよ。
- (3) 積に関する正則元を決定し、その逆元も求めよ。
- (4) 和と積が分配法則
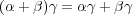 ,
,
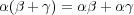 を満たすことを示せ。
を満たすことを示せ。
-- (1) 省略。
- (2)
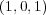 が単位元である。
が単位元である。
- (3)
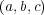 が正則元になるための必要条件として
が正則元になるための必要条件として
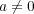 ,
,
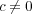 がすぐに分かる。
がすぐに分かる。
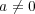 ,
,
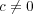 と仮定する。 このとき
と仮定する。 このとき
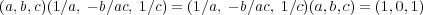 が確認できる。よって
が確認できる。よって
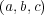 が 正則となるための必要十分条件は
が 正則となるための必要十分条件は
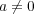 かつ
かつ
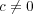 であることで、このとき逆元は
であることで、このとき逆元は
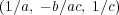 である。
である。
- (4) 計算によって確かめるだけなので省略する。
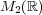 を実数を成分とする
を実数を成分とする
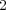 次正方行列全体の集合とする。
次正方行列全体の集合とする。
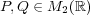 に対して
に対して
![[P,Q] = P Q - QP](img/algex35x.gif) によって二項演算を定める。これが結合法則を満たさないことを示せ。
-
によって二項演算を定める。これが結合法則を満たさないことを示せ。
-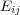 で
で
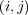 - 成分が
- 成分が
 で、他の成分がすべて
で、他の成分がすべて
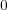 である
である
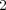 次正方行列を表すことにする。このとき
となり、結合法則は成り立たない。
次正方行列を表すことにする。このとき
となり、結合法則は成り立たない。![[[E11,E11],E12] = 0, [E11,[E11,E12]] = E12](img/algex754x.gif) (結合法則が成り立たないことを示すには、成り立たないような例を一つ挙げればよい。)
(結合法則が成り立たないことを示すには、成り立たないような例を一つ挙げればよい。)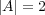 なる可換半群を一つ具体的に構成せよ。また
なる可換半群を一つ具体的に構成せよ。また
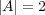 なる非可換な半群を一つ具体的に構成せよ。
-
なる非可換な半群を一つ具体的に構成せよ。
-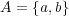 とする。任意の
とする。任意の
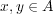 に対して
に対して
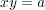 で定まるものは可換半群である。
で定まるものは可換半群である。
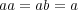 ,
,
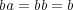 で定まるものは非可換半群である。
で定まるものは非可換半群である。
- 半群であるがモノイドではないものの例を一つ挙げよ。
-例えば、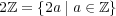 で演算として乗法を考えたもの。
で演算として乗法を考えたもの。
- モノイドであるが群ではないものの例を一つ挙げよ。
-例えば、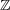 で演算として乗法を考えたもの。
で演算として乗法を考えたもの。
- モノイドの単位元はただ一つ存在することを示せ。
-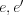 を共に単位元とする。このとき
を共に単位元とする。このとき
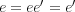 であるから
であるから
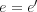 である。よって単位元はただ一つである。
である。よって単位元はただ一つである。
- モノイドの正則元に対して、その逆元はただ一つ存在することを示せ。
- を単位元とする。
を単位元とする。
 をモノイドの正則元とし
をモノイドの正則元とし
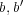 を共に
を共に
 の逆元とする。このとき
の逆元とする。このとき
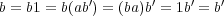 であるから
であるから
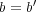 である。よって
である。よって
 の逆元はただ一つである。
の逆元はただ一つである。
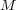 をモノイドとし、
をモノイドとし、
 を
を
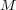 の正則元とする。写像
の正則元とする。写像
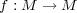 を
を
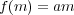 によって定めれば
によって定めれば
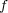 は全 単射であることを示せ。
-
は全 単射であることを示せ。
-(単射であること)
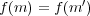 とする。
とする。
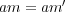 である。
である。
 は正則元なので、逆元
は正則元なので、逆元
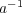 が存在する。
が存在する。
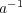 を
を
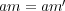 に左からかければ
に左からかければ
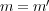 となる。よって
となる。よって
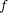 は単射である。
は単射である。
(全射であること)
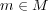 とする。このとき
とする。このとき
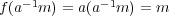 となるので
となるので
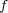 は全射である。
は全射である。
[別解]
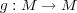 を
を
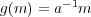 で定める。このとき
で定める。このとき
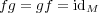 となるので
となるので
 は全単射である。
は全単射である。
 は通常の乗法によって半群になっている。このとき演算表 (乗法表) を
のように書く。
は通常の乗法によって半群になっている。このとき演算表 (乗法表) を
のように書く。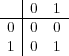
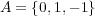 も通常の乗法によって半群になっている。この半群の乗法表を書け。
-
も通常の乗法によって半群になっている。この半群の乗法表を書け。
-
- (2)