距離空間論 演習問題 第12回
-
問題 1.
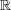 と
と
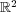 を通常の距離で距離空間とみなす。このとき
を通常の距離で距離空間とみなす。このとき
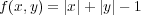 で定義される写像
が連続であることを示すことにより
で定義される写像
が連続であることを示すことにより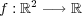 が
が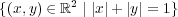
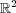 の閉集合であることを示せ。
の閉集合であることを示せ。
解答:
関数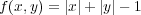 が連続であることを示せば
であり、
が連続であることを示せば
であり、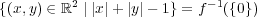
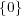 が
が
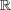 の閉集合であることから、考えている集合が閉集合であることが分かる。
連続性を示すためには、連続写像の和や合成が連続であることを使えばよい。
例えば、 写像
を
の閉集合であることから、考えている集合が閉集合であることが分かる。
連続性を示すためには、連続写像の和や合成が連続であることを使えばよい。
例えば、 写像
を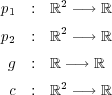 で定義すると、これらは全て連続であり
で定義すると、これらは全て連続であり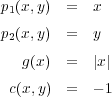 となる。よって
となる。よって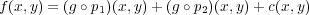
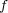 は連続である。
は連続である。
-
問題 2.
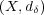 を離散距離空間とする。このとき任意の距離空間
を離散距離空間とする。このとき任意の距離空間
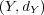 と任意の 写像
に対し
と任意の 写像
に対し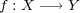
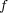 は連続であることを示せ。
は連続であることを示せ。
解説:
写像が連続であることを示すためには次の三つの方法がある:-
(a) 既知の連続写像の四則演算や合成による組み合わせで表わす
-
(b)
 -
-
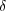 を用いる
を用いる
-
(c) 任意の開集合の逆像が開集合であることを示す
解答:
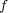 が連続であることを示すためには、任意の開集合
が連続であることを示すためには、任意の開集合
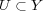 に対し
に対し
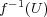 が
が
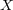 の開集合であることを示せばよい。
の開集合であることを示せばよい。
ところが 6/21 の演習問題 5 より、離散距離空間では全ての部分集合は開集合である。 よって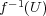 は
は
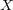 の開集合であり題意が示された。
の開集合であり題意が示された。
-
-
問題 3.
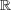 を通常の距離
を通常の距離
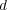 で距離空間とみなす。このとき
で距離空間とみなす。このとき
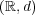 から離散距離空間
から離散距離空間
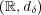 への恒等写像は連続ではないことを示せ。
への恒等写像は連続ではないことを示せ。
解答:
恒等写像をとおく。これが連続でないことを示すためには、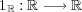
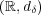 の開集合
の開集合
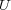 で
で
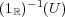 が
が
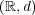 で開集合でないものを一つ見付ければよい。
で開集合でないものを一つ見付ければよい。
例えば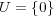 とすると、
とすると、
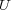 は離散距離では開集合であるが通常の Euclid 距離
は離散距離では開集合であるが通常の Euclid 距離
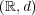 では開集合ではない。これで恒等写像が連続ではないことが示された。
では開集合ではない。これで恒等写像が連続ではないことが示された。
-
問題 4.
距離空間の間の写像に対し、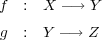
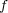 と
と
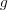 が一様連続ならば
が一様連続ならば
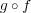 も一様連続であることを示せ。
も一様連続であることを示せ。
解答:
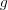 が一様連続であることから、任意の
が一様連続であることから、任意の
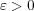 に対し
に対し
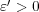 が存在し、任意の
が存在し、任意の
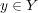 に対し
が成り立つ。この
に対し
が成り立つ。この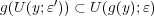
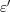 に対し、
に対し、
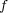 が一様連続であることから、
が一様連続であることから、
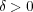 が存在し、任意の
が存在し、任意の
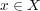 に対し
が成り立つ。よって任意の
に対し
が成り立つ。よって任意の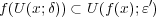
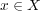 に対し
となり
に対し
となり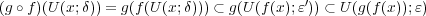
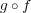 が一様連続であることが示された。
が一様連続であることが示された。
問題 5.
-
(a) 距離空間
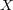 に対し
と定義する。
に対し
と定義する。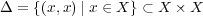
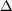 が
が
 の閉集合であることを示せ。
の閉集合であることを示せ。
-
(b) 連続関数に対し、そのグラフを
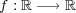 で定義する。このとき
で定義する。このとき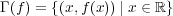
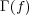 は
は
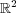 の閉集合であることを示せ。
の閉集合であることを示せ。
解説:
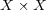 にどのように距離を定めるかを授業で説明していなかったので (a) は説明不足だった。
にどのように距離を定めるかを授業で説明していなかったので (a) は説明不足だった。
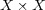 には以下のように距離を定め距離空間とみなす:
には以下のように距離を定め距離空間とみなす:
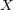 の距離関数を
の距離関数を
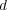 とするとき
を
とするとき
を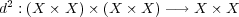 で定義する。これが距離関数の条件をみたすことはすぐ確かめられる。
で定義する。これが距離関数の条件をみたすことはすぐ確かめられる。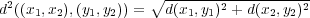
解答:
-
(a) 補集合が閉集合であることを示す。任意の
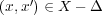 に対し、
に対し、
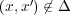 より
より
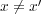 である。よって
とおくと、
である。よって
とおくと、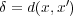
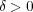 であり
とおくと
であり
とおくと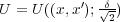
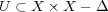 である。実際、
である。実際、
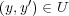 ならば
であるが、一般に
ならば
であるが、一般に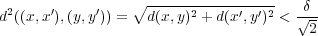
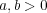 に対し相加相乗平均の公式より
であり
に対し相加相乗平均の公式より
であり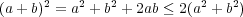 となる。ここで距離関数
となる。ここで距離関数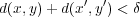
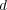 に関する三角不等式より
であるから
に関する三角不等式より
であるから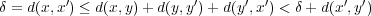 よって
よって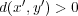
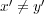 となり
となり
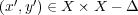 である。これで
が示され
である。これで
が示され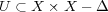
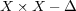 が開集合であることが分かった。
が開集合であることが分かった。
-
(b) (a) を用いる。写像を
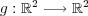 で定義すると、これは連続である。よって
で定義すると、これは連続である。よって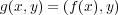
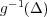 は閉集合である。こ こで
であるから
は閉集合である。こ こで
であるから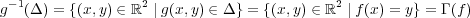
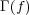 は閉集合であることが示された。
は閉集合であることが示された。
-
-
問題 6.
距離空間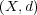 から
から
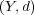 への写像
について次を示せ:
への写像
について次を示せ: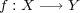
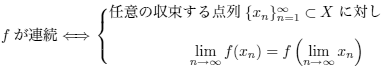
解答:
(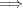 )
)
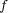 が連続であると仮定する。
が連続であると仮定する。
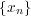 を
を
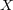 の収束する点列とし
とおく。このとき、任意の
の収束する点列とし
とおく。このとき、任意の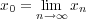
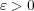 に対し
に対し
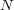 が存在し
を示せばよい。まず
が存在し
を示せばよい。まず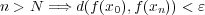
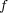 が連続であることから
となる
が連続であることから
となる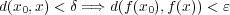
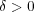 が存在する。この
が存在する。この
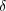 に対し、
に対し、
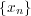 が
が
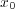 に収束することから、
に収束することから、
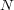 で
であるものが存在する。よって
で
であるものが存在する。よって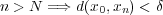 である。
である。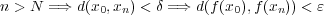
(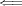 ) 背理法で示す。
) 背理法で示す。
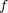 がある点
がある点
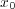 で連続でないと仮定する。するとある
で連続でないと仮定する。するとある
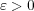 が存在し、任意の
が存在し、任意の
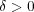 に対し
となる
に対し
となる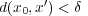 かつ
かつ
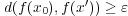
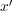 が存在する。そこで各
が存在する。そこで各
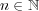 に対し
に対し
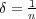 に対するそのような 点を一つ選び
に対するそのような 点を一つ選び
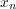 とする。すると
であるから
とする。すると
であるから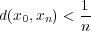
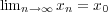 であるが、任意の
であるが、任意の
 に対し
であるから
に対し
であるから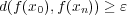
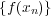 が
が
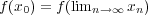 に収束することはない。
これは仮定に反する。よって
に収束することはない。
これは仮定に反する。よって
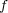 は連続である。
は連続である。
-
問題 7.
距離空間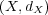 から
から
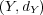 への写像
が任意の
への写像
が任意の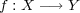
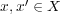 に対し
をみたすならば、一様連続であることを示せ。
に対し
をみたすならば、一様連続であることを示せ。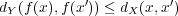
解答:
任意の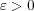 に対し
に対し
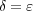 ととればよい。
ととればよい。
-
問題 8.
距離空間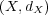 から
から
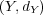 への一様連続写像
に対し
への一様連続写像
に対し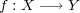
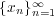 が
が
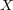 の Cauchy 列ならば
の Cauchy 列ならば
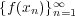 は
は
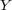 の Cauchy 列であることを示せ。
の Cauchy 列であることを示せ。
解答:
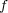 が一様連続であることから、任意の
が一様連続であることから、任意の
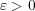 に対し
に対し
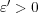 が存在し
となる。また
が存在し
となる。また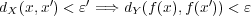
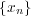 が Cauchy 列であることから、この
が Cauchy 列であることから、この
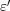 に対し
に対し
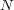 が存在 し
となる。併せれば、この
が存在 し
となる。併せれば、この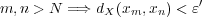
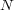 に対し
となり、
に対し
となり、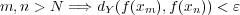
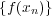 が Cauchy 列であることが示された。
が Cauchy 列であることが示された。