距離空間論 演習問題 第11回
-
問題 1.
次の Euclid 空間の部分集合それぞれのについて、有界か、閉集合か、そして compact かどうかを考えよ。- (a)
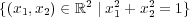
- (b)
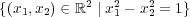
- (c)
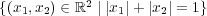
- (d)
 の部分集合として
の部分集合として
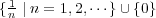
- (e)
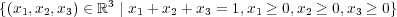
- (f)
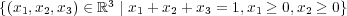
- (g)
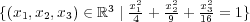
- (h)
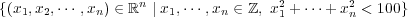
解説:
式で定義されている集合では、閉集合かどうかは や
や
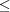 で定義されているかどうかをみるとよい。
正確には、次のことを用いる:
今、連続写像
で定義されているかどうかをみるとよい。
正確には、次のことを用いる:
今、連続写像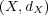 と
と
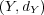 が距離空間で
が連続写像のとき、
が距離空間で
が連続写像のとき、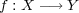
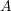 が
が
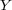 の閉集合ならば
の閉集合ならば
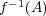 は
は
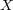 の閉集合である。
に対し
の閉集合である。
に対し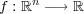
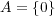 は
は
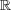 の閉集合だから
は閉集合となる。同様に
の閉集合だから
は閉集合となる。同様に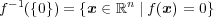
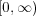 も
も
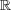 の閉集合だから
も閉集合になる。
の閉集合だから
も閉集合になる。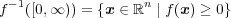
また考えている集合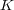 が有界であることを示すには
となる
が有界であることを示すには
となる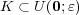
 を見付ければよい。逆に、有界ではないことを示すには、任意の
を見付ければよい。逆に、有界ではないことを示すには、任意の
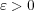 に対し
となる
に対し
となる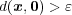
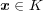 を見つければよい。または
となる
を見つければよい。または
となる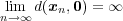
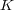 の中の点列
の中の点列
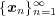 を見つければよい。
を見つければよい。
解答:
-
(a) 有界かつ閉集合、よって Heine-Borel の定理よりコンパクトである。(
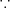 )
有界であることは、例えば
であることから分かる。閉集合であることは、連続関数
)
有界であることは、例えば
であることから分かる。閉集合であることは、連続関数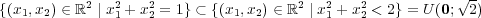 を「解説」のように用いれば分かる。
を「解説」のように用いれば分かる。
-
(b) 閉集合であるが有界でない。よって Heine-Borel の定理よりコンパクトではない。(
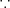 )
点列
は
)
点列
は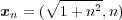
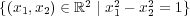 の中の点列であるが
である。よって有界ではない。
の中の点列であるが
である。よって有界ではない。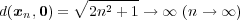
閉集合であることは、連続関数を「解説」のように用いれば分かる。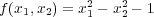
-
(c) 有界かつ閉集合、よって Heine-Borel の定理よりコンパクトである。(
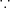 )
有界であることは
であることから分かる。
)
有界であることは
であることから分かる。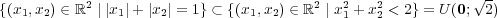
閉集合であることは、連続写像を「解説」のように用いれば分かる。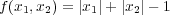
-
(d) 有界かつ閉集合、よって Heine-Borel の定理よりコンパクトである。(
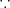 )
有界であることは
であることから分かる。
)
有界であることは
であることから分かる。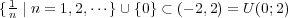
閉集合であることは、中間試験の問題だったから全員知っているはず。 -
(e) 有界かつ閉集合、よって Heine-Borel の定理よりコンパクトである。(
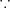 ) 有界であることは
であることから分かる。
) 有界であることは
であることから分かる。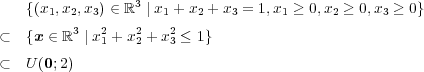
閉集合であることは次のように考えるとよい: 連続関数を用いて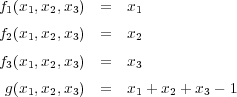 と定義すると、「解説」に書いたことからこれらは全て閉集合である。ま た
と定義すると、「解説」に書いたことからこれらは全て閉集合である。ま た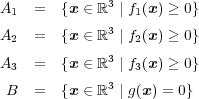 となり、閉集合の共通部分として閉集合であることが分かる。
となり、閉集合の共通部分として閉集合であることが分かる。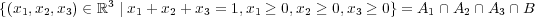
-
(f) 閉集合であるが有界でない。よって Heine-Borel の定理よりコンパクトではない。(
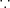 )
点列
はこの集合の元であるが
)
点列
はこの集合の元であるが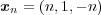 である。よって有界ではない。
である。よって有界ではない。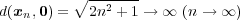
閉集合であることは、前問と同様にして示される。 -
(g) 有界かつ閉集合、よって Heine-Borel の定理よりコンパクトである。(
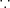 )
有界であることは
であることから分かる。
)
有界であることは
であることから分かる。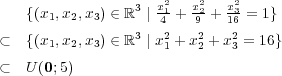
閉集合であることは、連続関数を「解説」のように用いれば分かる。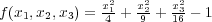
-
(h) コンパクトである。よって Heine-Borel の定理より有界かつ閉集合である。(
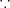 ) 原点からの距離が
) 原点からの距離が
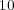 未満で全ての座標が整数の点は有限個しかない。 7/5 の演習問題 8 より、これはコンパクトである。
未満で全ての座標が整数の点は有限個しかない。 7/5 の演習問題 8 より、これはコンパクトである。
よって Heine-Borel の定理より有界閉集合となる。
- (a)
-
問題 2.
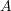 と
と
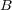 が距離空間
が距離空間
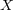 の部分集合で共に compact のとき
の部分集合で共に compact のとき
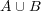 も compact になることを示せ。
も compact になることを示せ。
解答:
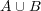 の開被覆
をとる。
の開被覆
をとる。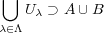 より、これは
より、これは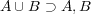
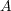 の開被覆でもあり、
の開被覆でもあり、
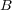 の開被覆でもある。
の開被覆でもある。
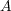 も
も
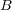 も compact だから
となる
も compact だから
となる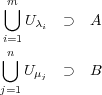 が取れる。このとき
が取れる。このとき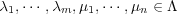 だから、元の開被覆から
だから、元の開被覆から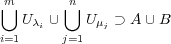
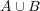 の有限開被覆が選べた。よって
の有限開被覆が選べた。よって
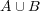 は compact である。
は compact である。
-
問題 3.
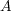 と
と
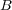 が距離空間
が距離空間
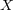 の部分集合で共に compact のとき
の部分集合で共に compact のとき
 も compact になることを示せ。
も compact になることを示せ。
解答:
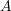 も
も
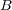 が compact だから閉集合になる。閉集合の共通部分は閉集合だから
が compact だから閉集合になる。閉集合の共通部分は閉集合だから
 も閉集合である。
も閉集合である。
ここで、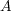 が compact で
が compact で
 がその閉部分集合だから、
がその閉部分集合だから、
 も compact である。
も compact である。
-
問題 4.
距離空間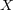 の部分集合の列
の部分集合の列
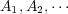 で各
で各
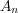 が compact であるが
が compact でない例を挙げよ。
が compact であるが
が compact でない例を挙げよ。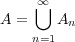
解答:
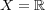 とし、通常の距離で距離空間と考える。各
とし、通常の距離で距離空間と考える。各
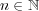 に対し
とする。このとき
に対し
とする。このとき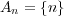
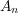 は有限集合だから compact である。しかし
は有界ではないので Heine-Borel の定理より compact ではない。
は有限集合だから compact である。しかし
は有界ではないので Heine-Borel の定理より compact ではない。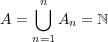
-
問題 5.
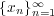 を距離空間
を距離空間
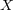 の収束する点列とし、その極限を
の収束する点列とし、その極限を
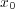 とする。このとき
は compact になることを示せ。
とする。このとき
は compact になることを示せ。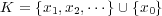
解答:
開被覆をとる。各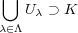
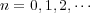 に対し
となる
に対し
となる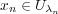
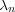 が存在する。特に
が存在する。特に
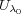 は
となる
は
となる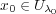
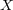 の開集合である。
の開集合である。
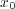 が内点であることから
となる
が内点であることから
となる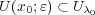
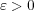 が存在するが
より、この
が存在するが
より、この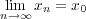
 に対し、
となる
に対し、
となる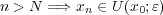
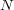 が存在する。つまり
である。よって
が存在する。つまり
である。よって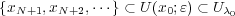 となり、元の開被覆から有限個を選んで
となり、元の開被覆から有限個を選んで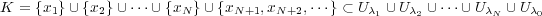
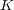 を覆うことができた。よって
を覆うことができた。よって
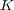 は compact である。
は compact である。
-
問題 6.
離散距離空間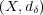 の部分集合
の部分集合
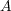 が compact ならば
が compact ならば
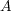 は有限集合であることを示せ。
は有限集合であることを示せ。
解答:
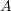 が compact であると仮定する。
離散距離空間では任意の部分集合が開集合であることから、一点から成る集合も開集合である。よって
は
が compact であると仮定する。
離散距離空間では任意の部分集合が開集合であることから、一点から成る集合も開集合である。よって
は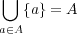
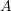 の開被覆である。
の開被覆である。
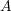 が compact ならば、この中から有限個を選んで
が compact ならば、この中から有限個を選んで
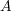 を覆えるはずであるが、各
を覆えるはずであるが、各
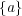 は異なる
は異なる
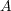 の点であるから、一つでも欠けると
の点であるから、一つでも欠けると
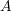 を覆うことはできない。つまり、もともと
を覆うことはできない。つまり、もともと
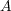 が有限集合でなければならない。
が有限集合でなければならない。