距離空間論 演習問題 第10回
-
問題 1.
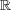 を
を
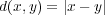 で距離空間と考える。このとき次の集合
で距離空間と考える。このとき次の集合
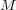 は compact ではないことを示せ:
は compact ではないことを示せ:
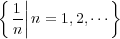
解答:
各 に対し
とおくと
に対し
とおくと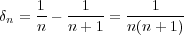 であり、
であり、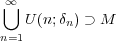
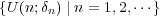 は
は
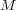 の (無限) 開被覆である。ところが
より
の (無限) 開被覆である。ところが
より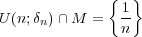
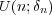 が一つでも欠けると
が一つでも欠けると
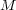 を覆うことができない。よって compact ではない。
を覆うことができない。よって compact ではない。
-
問題 2.
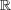 を
を
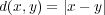 で距離空間と考える。開区間
で距離空間と考える。開区間
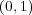 の場合を真似て
の場合を真似て
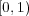 が compact ではないことを示せ。
が compact ではないことを示せ。
解答:
授業の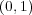 の例で用いた開被覆は
の例で用いた開被覆は
![(0,1]](img/answers10_17x.gif) を覆うものだった。
を覆うものだった。
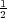 のところで折り返し
のところで折り返し
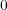 と
と
 を入れ替えれば compact の条件をみたさない被覆を得る。
を入れ替えれば compact の条件をみたさない被覆を得る。
 のところで折り返す写像は
だから、
のところで折り返す写像は
だから、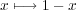 と定義すると
と定義すると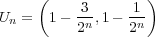 となり、
となり、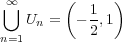
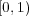 の開被覆を得る。しかし
の開被覆を得る。しかし
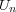 が欠けると
が欠けると
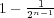 が覆えなくなるので、この中から有限個の開集合を選んで
が覆えなくなるので、この中から有限個の開集合を選んで
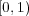 を覆うことはできない。よって
を覆うことはできない。よって
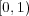 は compact ではない。
は compact ではない。
-
問題 3.
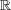 を
を
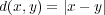 で距離空間と考える。このとき
で距離空間と考える。このとき
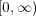 は compact ではないこと示せ。
は compact ではないこと示せ。
解答:
これも compact の条件をみたさない開被覆を見付ければよい。例えばとおけば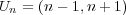
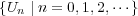 が求める開被覆になる。
が求める開被覆になる。
-
問題 4.
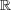 を
を
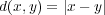 で距離空間と考える。このとき
で距離空間と考える。このとき
 は点列 compact ではないことを示せ。
は点列 compact ではないことを示せ。
解答:
収束しない部分列を含むような点列を一つ見付ければよい。 例えば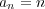 とおくと
とおくと
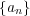 は収束しないし、そのどんな部分列も収束しない。
は収束しないし、そのどんな部分列も収束しない。
-
問題 5.
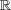 を離散距離空間と考える。このとき閉区間
を離散距離空間と考える。このとき閉区間
![[0,1]](img/answers10_41x.gif) は compact ではないこ とを示せ。
は compact ではないこ とを示せ。
解答:
各点![x ∈ [0,1]](img/answers10_42x.gif) に対し
とおく。このとき
に対し
とおく。このとき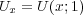
![{Ux | x ∈ [0,1]}](img/answers10_44x.gif) は
は
![[0,1]](img/answers10_45x.gif) の開被覆であるが
であるから、
の開被覆であるが
であるから、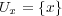
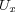 が一つでも欠けると
が一つでも欠けると
![[0,1]](img/answers10_48x.gif) を覆うことができない。
を覆うことができない。
![[0,1]](img/answers10_49x.gif) は無限集合だから、これは
は無限集合だから、これは
![{Ux | x ∈ [0,1]}](img/answers10_50x.gif) の中から有限個を選んで
の中から有限個を選んで
![[0,1]](img/answers10_51x.gif) を覆うことができないことを示している。よって
を覆うことができないことを示している。よって
![[0,1]](img/answers10_52x.gif) は compact ではない。
は compact ではない。
-
問題 6.
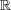 を
を
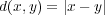 で距離空間と考える。このとき
で距離空間と考える。このとき
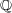 は compact か?
は compact か?
解答:
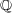 は閉集合ではないので compact ではない。
は閉集合ではないので compact ではない。
-
問題 7.
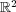 を通常の距離で距離空間と考える。このとき、次の集合は compact では ないことを示せ:
を通常の距離で距離空間と考える。このとき、次の集合は compact では ないことを示せ:
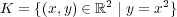
解答:
Heine-Borel の定理を使えば簡単であるが、ここでは定義を用いて直接証明する。各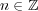 に対し
と定義する。これは
に対し
と定義する。これは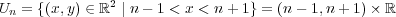
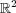 の開集合である。
より、これは
の開集合である。
より、これは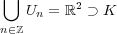
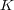 の開被覆である。
の開被覆である。
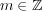 に対し
に対し
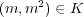 であるが、もしこの開被覆から
であるが、もしこの開被覆から
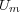 を除くと
となり
を除くと
となり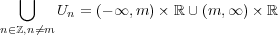
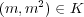 が含まれなくなり、
が含まれなくなり、
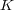 の開被覆でなくなってしまう。 このように、一つでも欠けると
の開被覆でなくなってしまう。 このように、一つでも欠けると
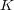 を覆えなくなる無限開被覆が存在するので
を覆えなくなる無限開被覆が存在するので
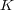 は compact ではない。
は compact ではない。
-
問題 8.
距離空間の有限個の点から成る部分集合は compact であることを示せ。解答:
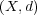 を距離空間とし
を距離空間とし
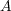 をその有限部分集合とする。
をその有限部分集合とする。
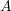 の元の個数(濃度)が
の元の個数(濃度)が
 として
とかく。
として
とかく。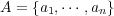
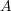 の任意の開被覆
について、この中から有限個の開集合を選んで
の任意の開被覆
について、この中から有限個の開集合を選んで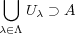
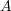 が覆えることを示せばよい。各
が覆えることを示せばよい。各
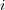 について、
について、
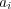 を含む
を含む
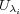 を一つづつ選んでくると
となり
を一つづつ選んでくると
となり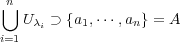
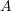 の有限開被覆となる。よって
の有限開被覆となる。よって
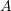 は compact である。
は compact である。
-
問題 9.
距離空間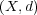 において、収束する点列
において、収束する点列
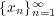 の任意の部分列も収束することを示せ。
の任意の部分列も収束することを示せ。
解答:
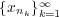 を部分列とする。このとき
を部分列とする。このとき
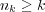 であることに注意する。
であることに注意する。
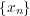 の収束先を
の収束先を
 とすると、任意の
とすると、任意の
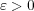 に対し、自然数
に対し、自然数
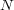 が存在し
となる。このとき
が存在し
となる。このとき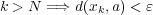
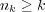 だから、
だから、
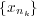 についても同じ
についても同じ
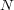 で
が成り立つ。これは
で
が成り立つ。これは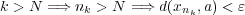
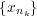 も
も
 に収束することを示している。
に収束することを示している。
-
問題 10.
距離空間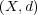 において、 Cauchy 列
において、 Cauchy 列
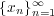 の任意の部分列は Cauchy 列であることを示せ。
の任意の部分列は Cauchy 列であることを示せ。
解答:
上の問題と同様なので省略。