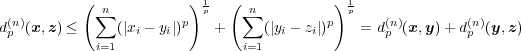距離空間論 演習問題 第9回
-
問題 1.
距離空間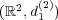 で考える。この距離空間において
の内部
で考える。この距離空間において
の内部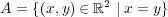
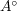 と閉包
と閉包
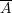 を求めよ。
を求めよ。
解答:
授業のときの例の真似をする。答えはである。まず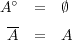
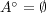 を示そう。もし元
を示そう。もし元
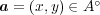 が存在したとすると、内部 の定義より
となる
が存在したとすると、内部 の定義より
となる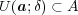
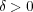 が存在する。ここで
が存在する。ここで
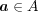 より
より
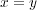 であり
であり
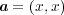 と書ける。 このとき
と書ける。 このとき
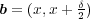 とおくと
より
とおくと
より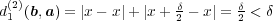
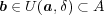 となるが、
となるが、
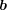 の
の
 座標と
座標と
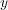 座標は異なるので
座標は異なるので
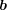 は
は
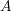 の元ではない。これは矛盾であり
の元ではない。これは矛盾であり
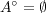 となる。
となる。
次に閉包を考える。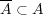 を示せばよいが、そのためには
を示せばよいが、そのためには
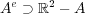 を示せば よい。
を示せば よい。
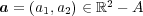 をとると、
をとると、
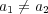 である。そこで
である。そこで
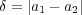 とおくと
とおくと
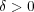 である。このとき
を示そう。実際
である。このとき
を示そう。実際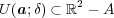
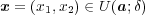 に対し
に対し
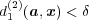 だから
である。ここで絶対値の三角不等式より
だから
である。ここで絶対値の三角不等式より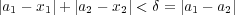 だから
だから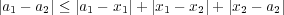 となる。よって
となる。よって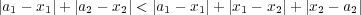
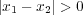 であり
であり
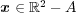 であることが示された。
であることが示された。
-
問題 2.
距離空間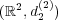 で考える。この距離空間において
の内部
で考える。この距離空間において
の内部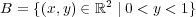
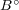 と閉包
と閉包
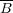 を求めよ。
を求めよ。
解答:
答えはである。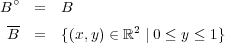
内部については、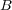 の任意の点が
の任意の点が
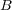 の内点であることを示せばよいが、実際
の内点であることを示せばよいが、実際
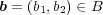 に対し
に対し
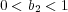 より
とおくと
より
とおくと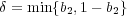
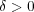 であり
であることが分かる。よって
であり
であることが分かる。よって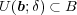
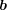 は
は
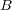 の内点である。
の内点である。
次に閉包を考えるために外部についてを示す。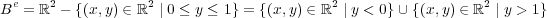
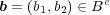 に対し
となる
に対し
となる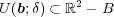
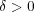 が存在する。このとき
が存在する。このとき
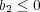 か
か
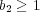 のどちらかであるが、
のどちらかであるが、
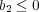 のとき
のとき
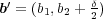 とおくと
とおくと
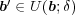 でありよって
でありよって
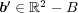 、つまり
となる。よって
、つまり
となる。よって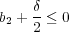 となる。
となる。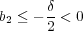
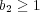 の場合、同様に
の場合、同様に
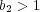 が示される。よって
が示され
が示される。よって
が示され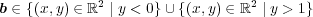 が分かった。
が分かった。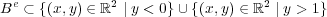
逆の包含関係を示すために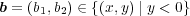 をとると、
をとると、
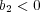 だから
だから
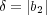 とおくと
とおくと
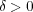 となり
となる。よって
となり
となる。よって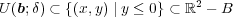
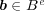 である。
である。
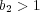 の場合も同様であり
が示される。
の場合も同様であり
が示される。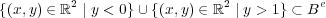
-
問題 3.
距離空間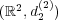 で考える。この距離空間において
の内部
で考える。この距離空間において
の内部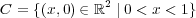
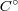 と閉包
と閉包
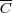 を求めよ。
を求めよ。
解答:
答えはである。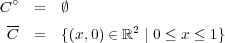
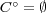 は問題 1 と同様に背理法で示される。閉包については、やはり補集合をとり
を示す。これは問題 2 と同様である。詳細は省略。
は問題 1 と同様に背理法で示される。閉包については、やはり補集合をとり
を示す。これは問題 2 と同様である。詳細は省略。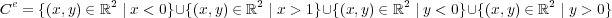
-
問題 4.
離散距離空間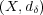 において次を示せ:
において次を示せ:
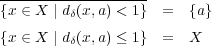
解答:
まず離散距離空間の定義から、任意の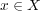 に対し
に対し
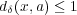 であ り
であることが分かる。また
であ り
であることが分かる。また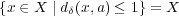 であるから
であるから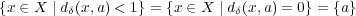 である。よって
である。よって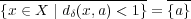
 を示せばよい。一般に
を示せばよい。一般に
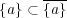 だから逆の包含関係を 示せばよい。
だから逆の包含関係を 示せばよい。
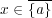 をとると、触点の定義より、任意の
をとると、触点の定義より、任意の
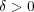 に対 し
であるが、特に
に対 し
であるが、特に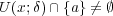
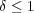 ととると
ととると
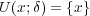 であり、
であり、
 となる。よって
となる。よって
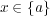 であり
が示された。
であり
が示された。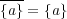
-
問題 5.
離散距離空間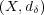 においては, 全ての部分集合が開集合であることを示せ。
においては, 全ての部分集合が開集合であることを示せ。
解答:
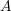 を
を
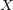 の部分集合とする。任意の
の部分集合とする。任意の
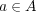 が
が
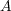 の内点であることを示せば よいが、これは
であることから分かる。
の内点であることを示せば よいが、これは
であることから分かる。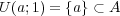
-
問題 6.
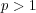 ,
,
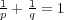 に対し, 関数
の増減を調べることにより,
に対し, 関数
の増減を調べることにより,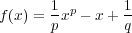
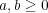 ,
,
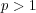 ,
,
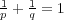 のとき次が成り立 つことを示せ:
のとき次が成り立 つことを示せ:
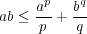
解答:
まず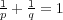 より
などの関係があることに注意する。
より
などの関係があることに注意する。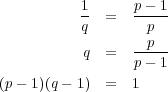
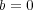 のときは、証明すべき不等式は自明だから
のときは、証明すべき不等式は自明だから
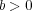 とする。証明すべき不等式の両辺を
とする。証明すべき不等式の両辺を
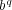 で割ると
となる。ここで
で割ると
となる。ここで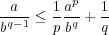 だから、結局
だから、結局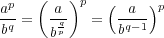
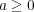 と
と
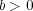 に対し
を示せばよい。
に対し
を示せばよい。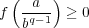
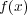 は
は
 に関し微分可能だから微分すると
となる。
に関し微分可能だから微分すると
となる。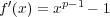
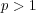 より、
より、
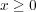 の範囲では
の範囲では
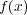 は
は
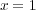 で極小値を持つのみ。と ころが
である。よって任意の
で極小値を持つのみ。と ころが
である。よって任意の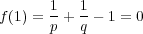
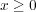 に対し
が示された。
に対し
が示された。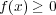
-
問題 7.
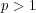 ,
,
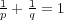 とする。
とする。
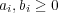 に対し
とおき,
に対し
とおき,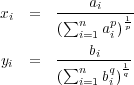
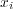 と
と
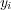 に対し上の問題の不等式を用いることにより
が成り立つことを示せ。
に対し上の問題の不等式を用いることにより
が成り立つことを示せ。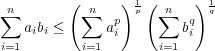
解答:
これは問題の指示通りに計算するだけなので省略。 -
問題 8.
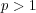 とする。
とする。
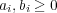 に対し
と変形し, 上の問題の不等式を用いることにより
に対し
と変形し, 上の問題の不等式を用いることにより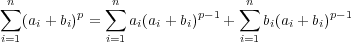 が成り立つことを示せ。
が成り立つことを示せ。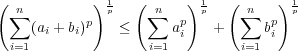
解答:
これも問題の指示通りに計算するだけなので省略。 -
問題 9.
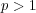 とする。上の問題を用いて
とする。上の問題を用いて
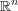 上で
が距離関数になることを確かめよ。
上で
が距離関数になることを確かめよ。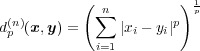
解答:
三角不等式以外は簡単なので省略。三角不等式については、まず絶対値の三角不等式よりが成り立つ。よって、まず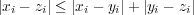 が分かる。ここで
が分かる。ここで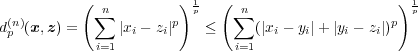 とおき、問題 8 の不等式を用いると
とおき、問題 8 の不等式を用いると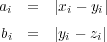 となり、三角不等式が示される。
となり、三角不等式が示される。