距離空間論 演習問題 第8回
-
問題 1.
写像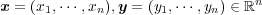 に対し
で定義するとき、これは metric になることを示せ。
に対し
で定義するとき、これは metric になることを示せ。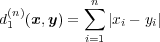
解答:
条件を順番に確かめるだけである:-
(a)
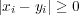 より
である。
より
である。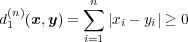
-
(b)
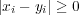 より
より
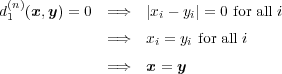
-
(c)
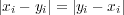 より
より
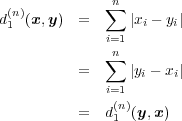
-
(d) 各
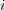 について絶対値の三角不等式より
よって
について絶対値の三角不等式より
よって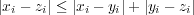 となり、三角不等式が証明できた。
となり、三角不等式が証明できた。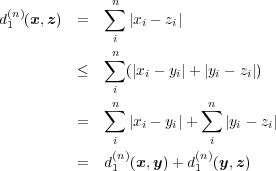
-
-
問題 2.
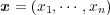 ,
,
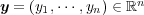 に対し
で定義するとき、これは metric になることを示せ。
に対し
で定義するとき、これは metric になることを示せ。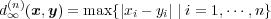 解答: これも順番に確かめるだけ:
解答: これも順番に確かめるだけ:-
(a)
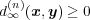 は
は
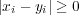 からすぐ分かる。
からすぐ分かる。
-
(b)
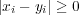 なので
なので
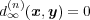 ならば全ての
ならば全ての
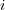 に つ い て
に つ い て
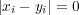 でなればならない。よって
でなればならない。よって
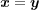 である。
である。
-
(c) これも
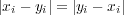 からすぐ分かる。
からすぐ分かる。
-
(d) 三角不等式はちょっと面倒である。まず絶対値の三角不等式よりが全ての
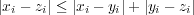
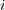 について成り立つ。よって
である。ここで
について成り立つ。よって
である。ここで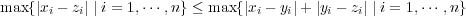 だから
だから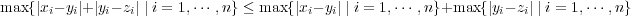 となる。
となる。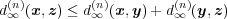
-
-
問題 3.
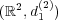 での原点を中心とした半径
での原点を中心とした半径
 の open ball を図示せよ。
の open ball を図示せよ。
解答:
定義よりである。ここで絶対値が場合分けで定義されていた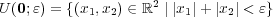 ことを思い出すと
ことを思い出すと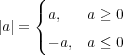 となる。これは直角二等辺三角形を 4 つ合わせた形であり図示すると次のようにな る。
となる。これは直角二等辺三角形を 4 つ合わせた形であり図示すると次のようにな る。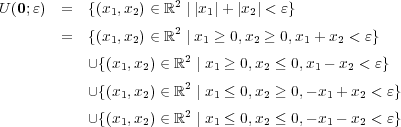 ただし境界は含まず内部のみ。
ただし境界は含まず内部のみ。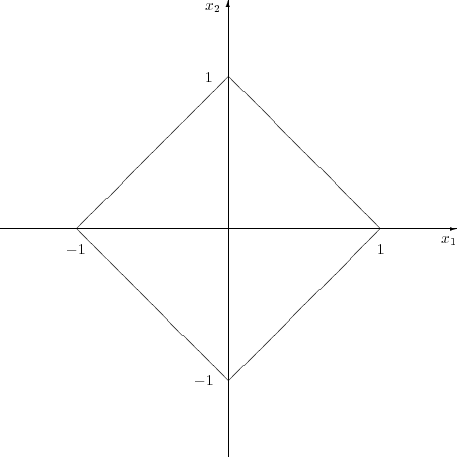
-
問題 4.
離散距離空間での open ball は何か?解答: 半径の値によって二種類ある。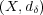 を離散距離空間とすると、
を離散距離空間とすると、
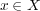 に対し
となる。
に対し
となる。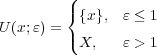
-
問題 5.
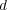 が集合
が集合
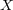 上の metric であるとき
も
上の metric であるとき
も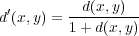
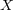 上の metric になることを示せ。
上の metric になることを示せ。
解答:
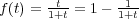 とおき、まずこの関数の性質を調べるとよい。
とおき、まずこの関数の性質を調べるとよい。
-
(a)
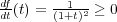 だから
だから
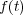 は単調増加である
は単調増加である
-
(b)
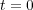 のとき
のとき
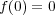 であり
であり
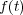 は単調増加だから
は単調増加だから
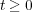 のとき
のとき
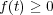 となる
となる
-
(c)
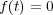 であるのは
であるのは
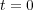 の場合に限る
の場合に限る
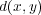 が metric であることから次のことが分かる:
が metric であることから次のことが分かる:
-
(a)
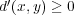
-
(c)
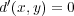
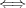
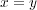
-
(d)
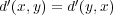
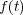 の性質を調べることによる分かる。まず
の性質を調べることによる分かる。まず
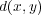 がmetricであることより
が成り立つ。ここで
がmetricであることより
が成り立つ。ここで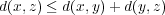
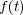 は単調増加だから
である。よって
は単調増加だから
である。よって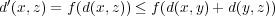
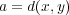 、
、
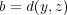 とおくとき
を示せばよい。これは以下のように証明できる:
とおくとき
を示せばよい。これは以下のように証明できる: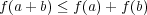 これで
これで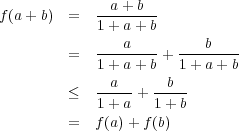
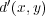 が metric であることが示された。
が metric であることが示された。
-
-
問題 6.
次は 上の metric になるか?
上の metric になるか?
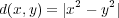
解答:
ならない。例えばであるが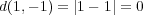
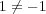 である。
である。
-
問題 7.
次は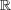 上の metric になるか?
上の metric になるか?
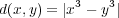
解答:
なる。証明は簡単なので省略。 -
問題 8.
次は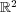 上の metric になるか?
ただし
上の metric になるか?
ただし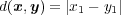
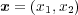 で
で
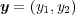 である。
である。
解答:
ならない。例えば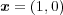 、
、
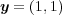 とすると
であるが
とすると
であるが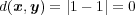
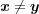 である。
である。