距離空間論 演習問題 第7回
-
問題 1.
写像と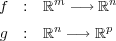
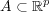 に対し
であることを確かめよ。
に対し
であることを確かめよ。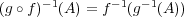
解答:
二つの集合が等しいことを示すのだからを示せばよい。これには、逆像と写像の合成の定義を用いるだけ:
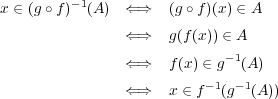
-
問題 2.
写像を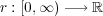
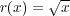 で定義する。
で定義する。
-
(a)
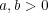 に対し
に対し
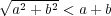 を示せ。
を示せ。
-
(b) 任意の
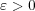 に対し
に対し
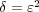 とおく。任意の
とおく。任意の
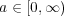 に対し
であることを確かめることにより、
に対し
であることを確かめることにより、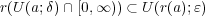
 が一様連続であることを示せ。
が一様連続であることを示せ。
解答:
-
(a)これは (b) のためのヒントなので省略。
-
(b)
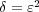 とおくと、任意の
とおくと、任意の
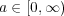 に対し
よって(a)を用いて
に対し
よって(a)を用いて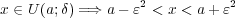 を得る。同様に
を得る。同様に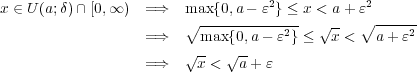 が示され
が示され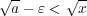 が分かる。よって
が分かる。よって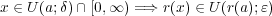 であり、
であり、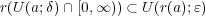
 は
は
 に無関係であるから一様連続である。
に無関係であるから一様連続である。
-
-
問題 3.
写像を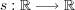
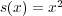 で定義すると一様連続ではないことを示せ。
で定義すると一様連続ではないことを示せ。
解答:
背理法で示す。 が一様連続であると仮定すると、任意の
が一様連続であると仮定すると、任意の
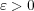 に対し
に対し
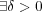 s.t. 任意の
s.t. 任意の
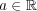 に対し
が成り立つ。
に対し
が成り立つ。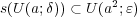
 は任意だから
は任意だから
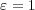 と取る。このとき、任意の
と取る。このとき、任意の
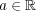 に対 し
が成り立つ
に対 し
が成り立つ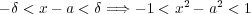
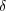 が存在するはずである。
そこで
が存在するはずである。
そこで
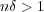 となる自然数
となる自然数
 をとり
をとり
 とする。また
とする。また
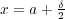 とす ると
が成り立っている。ところが
とす ると
が成り立っている。ところが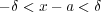 であり
であり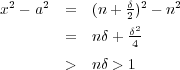
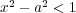 に矛盾。
に矛盾。
よって は一様連続ではない。
は一様連続ではない。
-
問題 4.
連続写像と定数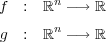
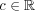 に対し
で定義される写像
に対し
で定義される写像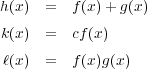 は全て連続であることを示せ。
は全て連続であることを示せ。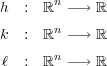
解答:
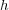 の場合:
の場合:
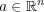 をとり
をとり
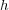 が
が
 で連続であることを示す。
で連続であることを示す。
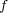 と
と
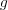 の連続 性より、任意の
の連続 性より、任意の
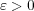 に対し
となる
に対し
となる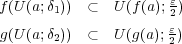
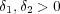 が存在する。このとき
とおくと
が存在する。このとき
とおくと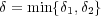 よって
よって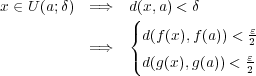
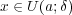 に対し
である。これで
に対し
である。これで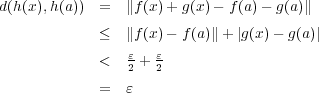
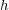 が連続であることが示された。
が連続であることが示された。
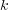 の場合: まず
の場合: まず
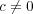 の場合を考える。
の場合を考える。
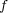 の連続性より、任意の
の連続性より、任意の
 に対し
となる
に対し
となる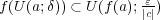
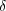 が存在する。このとき
であり、
が存在する。このとき
であり、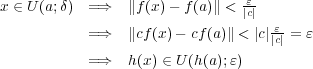
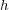 は
は
 で連続になる。
で連続になる。
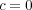 の場合、
の場合、
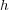 は
となる定値写像であり、常に
は
となる定値写像であり、常に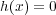 となる。よってどんな
となる。よってどんな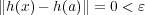
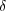 をとってもよく、連続になる。
をとってもよく、連続になる。
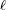 の場合: 任意の
の場合: 任意の
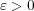 に対し
とおく。
に対し
とおく。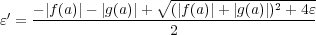
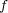 と
と
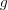 の連続性から
となる
の連続性から
となる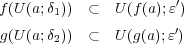
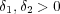 が存在する。このとき
が存在する。このとき
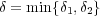 とおくと
とおくと
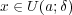 に 対し
となる。よって
に 対し
となる。よって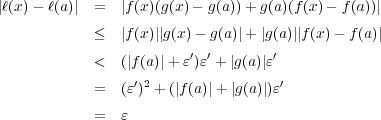 となる。
となる。