距離空間論 演習問題 第6回
-
問題 1.
次の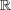 の部分集合の集積点は何か?また孤立点は何か?(答えだけでよい)
の部分集合の集積点は何か?また孤立点は何か?(答えだけでよい)
- (a)
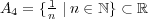
- (b)
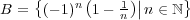
- (c)
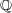
解答:
集積点を求めるには、閉包を考えるか収束する点列を探すかすればよい。孤立点はその集合の元を個別に調べればよい。-
(a)集積点は
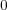 。孤立点
。孤立点
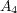 の点全て。
の点全て。
-
(b)集積点は
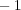 と
と
 。孤立点は
。孤立点は
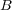 の点全て。
の点全て。
-
(c)集積点は
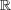 の点全て。孤立点は無し。
の点全て。孤立点は無し。
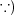 集積点ならば触点である。5月1 日の演習問題8より閉包は
である。この中から集積点を見付ければよい。全ての
集積点ならば触点である。5月1 日の演習問題8より閉包は
である。この中から集積点を見付ければよい。全ての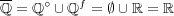
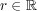 が集積点で あることを示そう。教科書 p.34 定理 1.4 より、任意の自然数
が集積点で あることを示そう。教科書 p.34 定理 1.4 より、任意の自然数
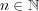 に対し
となる有理数
に対し
となる有理数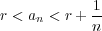
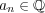 が存在する。このとき
が存在する。このとき
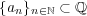 であり
だから、
であり
だから、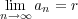
 は
は
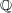 の集積点である。よって
の集積点である。よって
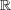 の元は全て
の元は全て
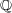 の集積点。
以上のことから、
の集積点。
以上のことから、
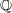 の元は全て集積点になってしまうので孤立点はない。
の元は全て集積点になってしまうので孤立点はない。
- (a)
-
問題:
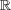 の部分集合として,
の部分集合として,
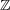 の全ての点は孤立点であることを示せ。
の全ての点は孤立点であることを示せ。
解答:
任意の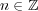 に対し
に対し
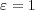 ととれば
となる。よって全ての
ととれば
となる。よって全ての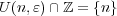
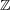 の点は孤立点。
の点は孤立点。
-
問題 3.
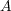 が
が
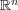 の有限個から成る部分集合なら
の有限個から成る部分集合なら
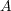 の点は全て孤立点であることを 示せ。
の点は全て孤立点であることを 示せ。
解答:
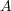 の濃度を
の濃度を
 として
とおく。
として
とおく。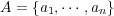
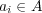 に対し
とおくと、
に対し
とおくと、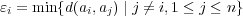
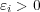 であり
である。よって
であり
である。よって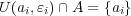
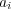 は孤立点である。
は孤立点である。
-
問題 4.
写像を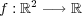 で定義するとき, この写像について次の問に答えよ:
で定義するとき, この写像について次の問に答えよ: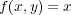
- (a)
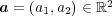 と
と
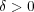 に対し, 集合
に対し, 集合
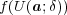 を求めよ。
を求めよ。
- (b)
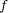 は連続であることを示せ。
は連続であることを示せ。
解答:
-
(a)定義よりである。ここで
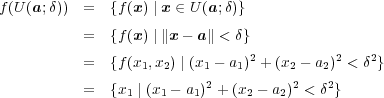
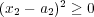 より
であり
より
であり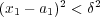 よって
よって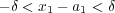 である。
である。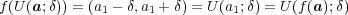
-
(b)
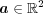 をとる。任意の
をとる。任意の
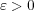 に対し
とおく。すると(a)より
に対し
とおく。すると(a)より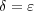 より
より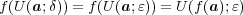 となり
となり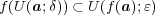
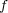 は点
は点
 で連続である。
で連続である。
 は任意だったから
は任意だったから
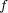 は連続である。
は連続である。
- (a)
-
問題 5.
写像を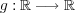 で定義するとき, この写像について次の問に答えよ:
で定義するとき, この写像について次の問に答えよ: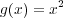
-
(a)
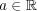 と
と
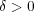 に対し, 集合
に対し, 集合
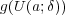 を求めよ。
を求めよ。
(ヒント: 場合分けが必要) -
(b)
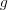 は連続であることを示せ。
は連続であることを示せ。
解答:
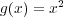 が連続であることを示すだけなら
が連続であることを示すだけなら
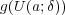 を求める必要はない。練習のために (a) を設けた。
を求める必要はない。練習のために (a) を設けた。
-
(a)定義よりである。
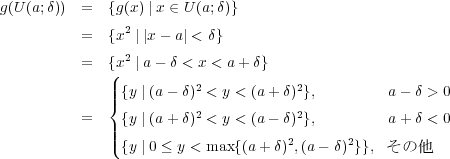
-
(b)
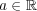 をとる。
をとる。
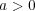 と
と
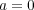 と
と
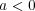 の三つの場合があるが、
の三つの場合があるが、
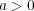 と
と
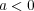 の場合は同様なので、まず、
の場合は同様なので、まず、
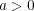 の場合について考える。任意の
の場合について考える。任意の
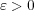 に対し
とおく。ここで
に対し
とおく。ここで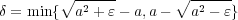
 は十分小さいと仮定してよいので、
は十分小さいと仮定してよいので、
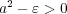 と仮定する。 このとき
であるから、(a) の結果より
と仮定する。 このとき
であるから、(a) の結果より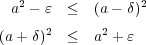 となる。
となる。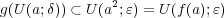
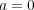 のときは
のときは
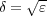 ととればよい。
ととればよい。
-
-
問題 6.
写像を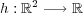 で定義するとき, この写像について次の問に答えよ:
で定義するとき, この写像について次の問に答えよ: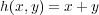
-
(a)
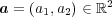 と
と
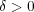 に対し, 集合
に対し, 集合
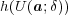 を求めよ。
を求めよ。
-
(b) 任意の
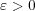 に対し
に対し
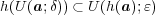 となる
となる
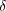 が存在すること を示せ。
が存在すること を示せ。
解答:
-
(a)定義よりここで、条件
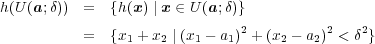
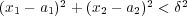 の元での
の元での
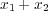 の最大値最小値は、それぞれ
の最大値最小値は、それぞれ
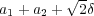 と
と
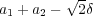 であることが分かる。(例えば相加相乗平均の公式)よって
であることが分かる。
であることが分かる。(例えば相加相乗平均の公式)よって
であることが分かる。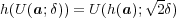
-
(b)任意の
 に対し
に対し
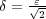 ととればよい。
ととればよい。
-