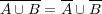距離空間論 演習問題 第5回
-
問題 1.
次の の部分集合の中から開集合と閉集合を選べ (答だけでよい):
の部分集合の中から開集合と閉集合を選べ (答だけでよい):
![A2 = [a,∞ ), A4 = {1n | n ∈ ℕ},A6 = [1,2]∪ [4,5], A8 = [2,5]∪ {7},A = ℝ- ℤ, A = {--1- | x ∈ ℝ} 9 14 x2+1](img/answers5_1x.gif)
解答:
それぞれの集合について調べると以下の通り:開集合 閉集合 
× ○ 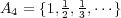
× × 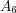
○ × 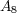
○ × 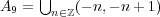
× ○ ![A14 = (0,1]](img/answers5_7x.gif)
× × -
問題 2.
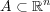 に対し次を示せ:
に対し次を示せ:
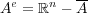
解答:
内部、外部、境界についてであり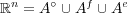 である。よって
である。よって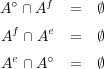 ここで
ここで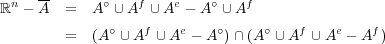 である。同様に
である。同様に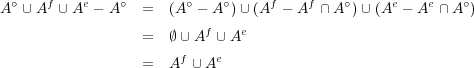 であり、よって
であり、よって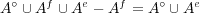 となる。
となる。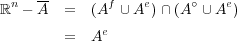
-
問題 3.
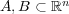 に対し次を示せ:
また
に対し次を示せ:
また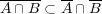
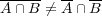 である例を挙げよ。
である例を挙げよ。
解答:
まず一般にが成り立つから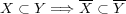 である。よって
である。よって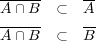 である。
である。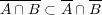
例としては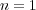 のときの
が分かりやすい。このとき
のときの
が分かりやすい。このとき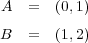 である。
である。![A∩-B--= ∅ = ∅-- --A∩ B = [0,1]∩ [1,2] = {1}](img/answers5_24x.gif)
一般の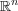 でも例を作ることができる。
でも例を作ることができる。
-
問題 4.
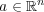 に対し一点から成る集合
に対し一点から成る集合
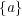 の閉包は何か? (答だけでなく証明もす ること)
の閉包は何か? (答だけでなく証明もす ること)
解答:
答えはである。証明は以下の通り: まず一般に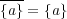 であるから
であるから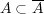 を示せばよい。
を示せばよい。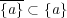
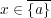 を取ると、
を取ると、
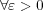 に対し
である。ところが
に対し
である。ところが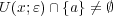 だから、これが空集合でないとすると
だから、これが空集合でないとすると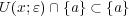 である。これは
である。これは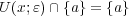
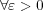 に対し
であることを意味する。よって実数の性質より
に対し
であることを意味する。よって実数の性質より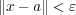 となり、
となり、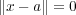
 となる。つまり
が示された。
となる。つまり
が示された。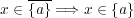
-
問題 5.
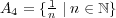 の閉包は何か? (答だけでなく証明もすること)
の閉包は何か? (答だけでなく証明もすること)
解答:
答えはである。証明は以下の通り: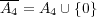 であり、また
であり、また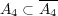
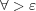 に対し
に対し
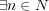 s.t.
である。つまり
s.t.
である。つまり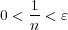 であり
であり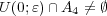
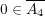 である。
である。
逆に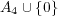 以外の点が
以外の点が
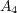 の触点でないことを示す。
の触点でないことを示す。
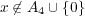 には次の三つの場合がある:
には次の三つの場合がある:
- (a)
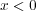
- (b)
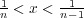
- (c)
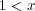
とおけば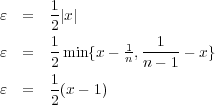 となるので、これらの点は触点ではない。
となるので、これらの点は触点ではない。
- (a)
-
問題 6:
次の集合が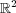 の開集合であることを示せ:
の開集合であることを示せ:
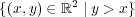
解答:
5/10 の問題 6 よりである。よって開集合。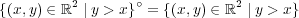
-
問題 7.
次の集合が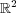 の閉集合であることを示せ:
の閉集合であることを示せ:
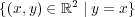
解答:
一般に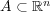 に対し
である。問題 6 より
に対し
である。問題 6 より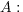 閉集合
閉集合
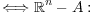 開集合
は開集合であり、同様に
開集合
は開集合であり、同様に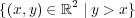 も開集合である。よってその和集合
も開集合である。よってその和集合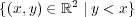 も開集合であり、その補集合
も開集合であり、その補集合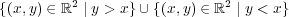 は閉集合である。
は閉集合である。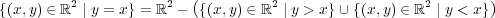
-
問題 8.
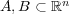 が開集合のとき
が開集合のとき
 も開集合であることを示せ。
も開集合であることを示せ。
解答:
一般にである。ここで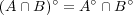
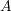 と
と
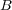 が開集合ならば
であり
が開集合ならば
であり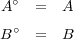 となる。よって
となる。よって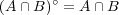
 は開集合である。
は開集合である。
-
問題 9.
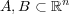 が閉集合のとき
が閉集合のとき
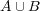 も閉集合であることを示せ。
も閉集合であることを示せ。
解答:
等式を使えば、問題 8と同様である。