距離空間論 演習問題 第4回
-
問題 1.
![B = [a,b]](img/answers4_0x.gif) に対し次を示せ:
に対し次を示せ:
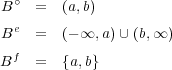
解答:
まず内部を考えよう。集合の等式を示すのだからを示す。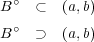
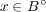 なら
である。
なら
である。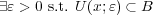
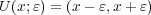 より
より
![(x - ε,x + ε) ⊂ B = [a,b]](img/answers4_6x.gif) となる。これは
ということ。よって
となる。これは
ということ。よって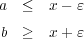 となり、
となり、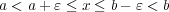
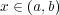 、よって
である。
、よって
である。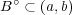
逆に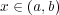 とする、つまり
とする。
とする、つまり
とする。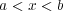
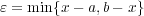 とおくと
であり、
とおくと
であり、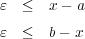
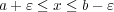 だから
よって
だから
よって![U (x,ε) = (x- ε,x+ ε) ⊂ [a,b] = B](img/answers4_16x.gif)
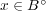 となる。これで
となる。これで
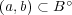 が示され、
が示され、
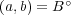 が証明された。
が証明された。
外部は、内部とほとんど同じなので省略。
内部と外部が分かれば、境界は分かる: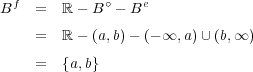
-
問題 2:
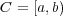 について、その内部、外部、境界は何になるか?
について、その内部、外部、境界は何になるか?
解答:
問題 1のようにやってもよいが、以下のようにすると楽である。より![(a,b) ⊂ [a,b) ⊂ [a,b]](img/answers4_22x.gif) となる。ここで
となる。ここで![∘ ∘ ∘(a,b) ⊂ [a,b) ⊂ [a,b]](img/answers4_23x.gif) だから
だから![(a,b)∘ = (a,b) ∘[a,b] = (a,b)](img/answers4_24x.gif)
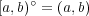 となる。
となる。
同様に![[a,b)e = (a,b)e = [a,b]e = (- ∞, a)∪ (b,∞ )](img/answers4_26x.gif) が示せる。
が示せる。
よってである。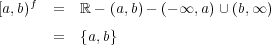
-
問題 3.
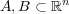 に対し次を示せ:
また
に対し次を示せ:
また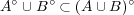
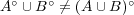 である例を挙げよ。
である例を挙げよ。
解答:
まずより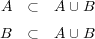 となる。よって
となる。よって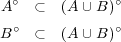 である。
である。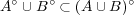
例としてはがある。![A = [- 1,0]B = [0,1]](img/answers4_34x.gif)
-
問題 4.
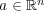 と
と
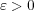 に対し
に対し
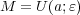 とする。このとき次を示せ:
とする。このとき次を示せ:
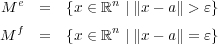
解答:
外部について考える。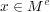 ならば
すなわち
ならば
すなわち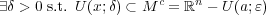 である。言い替えると
である。言い替えると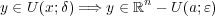 となる。ここで
となる。ここで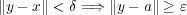 とおくと
とおくと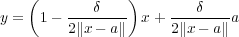 であり
であり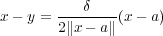 だから
だから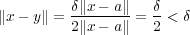 が成り立つはずである。よって
が成り立つはずである。よって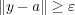 より
より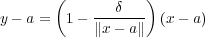 となり
となり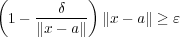 つまり
つまり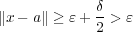
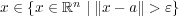 が示された。
が示された。
逆に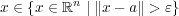 のとき
とすると
のとき
とすると
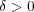 であり
となることが分かる。よって
であり
となることが分かる。よって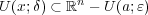 が言えた。
が言えた。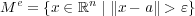 と合わせて
と合わせて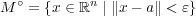 となる。
となる。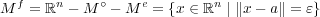
-
問題 5.
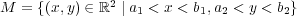 とする。このとき
とする。このとき
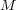 の内部、外部、境界を求めよ。
の内部、外部、境界を求めよ。
解答:
答えは以下のようになる。「かつ」と「または」に注意すること:証明は省略。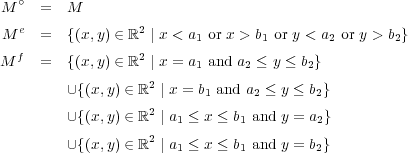
-
問題 6.
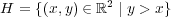 の内部、外部、境界は何か?
の内部、外部、境界は何か?
解答:
答えは以下のようになる:証明は以下の通り。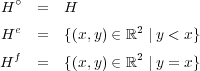
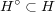 であるから, 任意の
であるから, 任意の
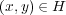 が内点であることを示す。
が内点であることを示す。
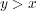 より
より
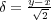 とおくと
とおくと
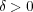 であり
となる。よって
であり
となる。よって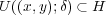
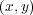 は
は
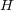 の内点である。同様に
が示せる。よって
の内点である。同様に
が示せる。よって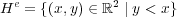 である。
である。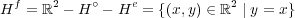
-
問題 7:
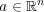 に対し一点から成る集合
に対し一点から成る集合
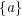 の内部、外部、境界は何か?
の内部、外部、境界は何か?
解答:
答えは以下のようになる:証明は以下の通り。まず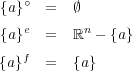
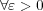 に対し
であるから
に対し
であるから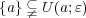
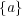 の内点は存在しない。よって
である。また
の内点は存在しない。よって
である。また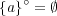 であるが、任意の
であるが、任意の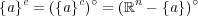
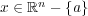 に対し
とおくと
に対し
とおくと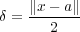 となる。よって
となる。よって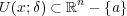 となり
となり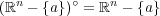 である。以上のことより
である。以上のことより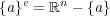 となる。
となる。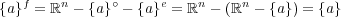
-
問題 8:
有理数の集合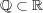 に対し次を確かめよ:
に対し次を確かめよ:
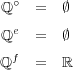
解答:
任意の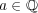 と
と
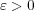 に対し
となる
に対し
となる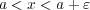
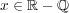 が存在する。よって
となる
が存在する。よって
となる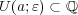
 は存在しない。つまり
は存在しない。つまり
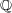 の内点は存在しない。よって
である。同様の理由で
の内点は存在しない。よって
である。同様の理由で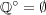 となる。よって
となる。よって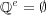 となる。
となる。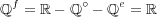
-
問題 9:
空集合の内部、外部、境界は何か?解答:
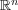 で考える。答えは以下のようになる:
証明は以下の通り。まず一般に
で考える。答えは以下のようになる:
証明は以下の通り。まず一般に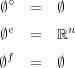
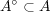 であるから,
であるから,
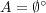 とすると
である。これは
とすると
である。これは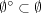
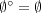 であることを意味する。次に
であるが,
であることを意味する。次に
であるが,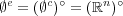
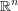 の点は全て内点であり
の点は全て内点であり
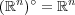 , よって
である。よって
, よって
である。よって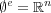 となる。
となる。