距離空間論 演習問題 第3回
-
問題 1.
次の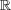 の部分集合の上限,下限,最大値,最小値を(もし存在するなら)求めよ:
の部分集合の上限,下限,最大値,最小値を(もし存在するなら)求めよ:
- (a)
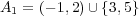
- (b)
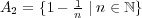
- (c)
![A = [- 5,2]∩ [1,4]c 7](img/answers3_3x.gif)
- (d)
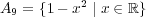
解答:
一般に次のことを使うとよい: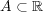 について
について
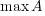 が存在する
が存在する
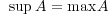
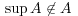
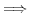
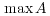 は存在しない
は存在しない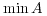 が存在する
が存在する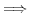
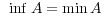
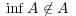
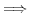
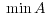 は存在しない
は存在しない-
(a)
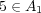 かつ
かつ
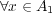 に対し
に対し
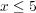 であるから
であるから
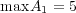 、よって
、よって
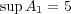 である。
である。
次に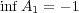 を示す。まず任意の
を示す。まず任意の
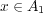 に対し
に対し
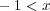 である。また任意の
である。また任意の
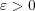 に対し
とする。このとき
に対し
とする。このとき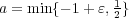
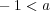 であるから実数の性質により
となる有理数
であるから実数の性質により
となる有理数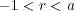
 が存在する。
が存在する。
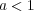 より
より
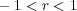 であり、よって
であり、よって
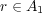 である。また
である。また
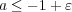 であり
となる。よって
であり
となる。よって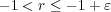 である。
である。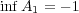
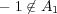 より
より
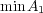 は存在しない。
は存在しない。
-
(b)
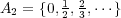 である。
である。
よって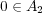 でありかつ
でありかつ
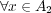 に対し
に対し
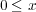 であるから
であるから
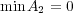 、よって
、よって
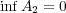 である。
である。
次に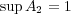 を示す。まず任意の
を示す。まず任意の
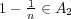 に対し
に対し
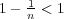 である。また実数の性質より、任意の
である。また実数の性質より、任意の
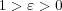 に対し
となる整数
に対し
となる整数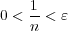
 が存在する。(Archimedesの定理) よって
となるが、
が存在する。(Archimedesの定理) よって
となるが、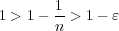
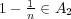 であるから、これは
であるから、これは
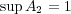 を意味する。
を意味する。
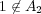 より
より
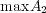 は存在しない。
は存在しない。
-
(c)
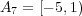 である。
である。
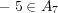 より
より
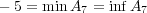 である。
である。
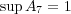 の証明は省略。
の証明は省略。
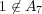 より
より
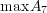 は存在しない。
は存在しない。
-
(d)
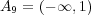 である。
である。
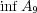 も
も
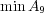 も存在しない。
も存在しない。
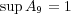 の証明は省略。
の証明は省略。
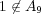 より
より
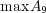 は存在しない。
は存在しない。
- (a)
-
問題 2.
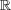 の部分集合
の部分集合
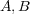 について次を示せ:
について次を示せ:
-
(a)
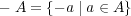 とおくとき,
とおくとき,
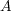 が上に有界ならば
が上に有界ならば
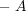 は下に有界であり
また,
は下に有界であり
また,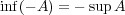
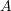 が下に有界ならば
が下に有界ならば
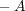 は上に有界であり
は上に有界であり
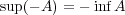
-
(b)
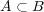 のとき
のとき
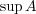 と
と
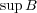 が共に存在するなら
また,
が共に存在するなら
また,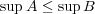
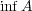 と
と
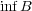 が共に存在するなら
が共に存在するなら
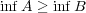
解答:
-
(a) 不等号の向きを変えるだけなので前半だけ証明する。
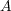 が上に有界とすると
よって
が上に有界とすると
よって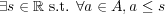 となり
となり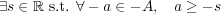
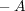 が下に有界となる。
が下に有界となる。
次に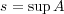 とすると
であり、これは
とすると
であり、これは
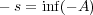 を意味する。
を意味する。
-
(b) これも
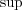 の場合だけ示す。
の場合だけ示す。
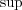 の定義から
であるが、
の定義から
であるが、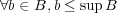
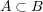 であるから
である。よって
であるから
である。よって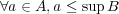
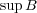 は
は
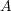 の上界の一つであり、
の上界の一つであり、
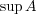 は
は
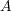 の上界の最小 値だったから
である。
の上界の最小 値だったから
である。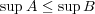
-
-
問題 3:
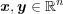 に対し
とおくと次が成り立つことを示せ:
に対し
とおくと次が成り立つことを示せ: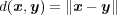
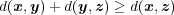
解答:
これは次の線形代数の知識を確認するための問題である: 任意の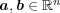 に対し
問題で
に対し
問題で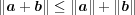 とおき上の不等式を用いるとよい。
とおき上の不等式を用いるとよい。
-
問題 4:
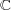 が順序体ではないことを示せ。
が順序体ではないことを示せ。
解答:
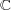 が順序体であると仮定し矛盾を導く。
が順序体であると仮定し矛盾を導く。
まず順序体の定義から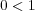 であることを示す。
(このことを証明していな い人が多かった。これは当たり前ではない。順序体の定義を使って証明すべきこと。)
であることを示す。
(このことを証明していな い人が多かった。これは当たり前ではない。順序体の定義を使って証明すべきこと。)
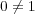 より
より
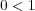 または
または
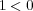 のいづれかが成り立つ。もし
のいづれかが成り立つ。もし
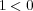 だとすると、両辺に
だとすると、両辺に
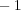 を加え
となる。よって不等式の両辺に
を加え
となる。よって不等式の両辺に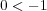
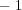 をかけても不等号の向きは変らない。特 に、この不等式の両辺に
をかけても不等号の向きは変らない。特 に、この不等式の両辺に
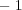 をかけると
となり
をかけると
となり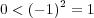
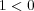 という仮定に矛盾。よって
という仮定に矛盾。よって
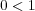 である。
また
である。
また
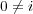 より
より
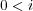 または
または
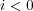 のいづれかが成り立つ。
のいづれかが成り立つ。
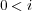 のとき、 両辺に
のとき、 両辺に
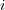 をかけると
となり矛盾。
をかけると
となり矛盾。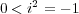
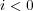 のとき、両辺に
のとき、両辺に
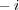 を加えて
である。この不等式の両辺に
を加えて
である。この不等式の両辺に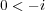
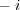 をかけて
となりやはり矛盾。
をかけて
となりやはり矛盾。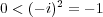
これは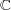 が順序体であるという仮定が間違っていることを意味している。
よって
が順序体であるという仮定が間違っていることを意味している。
よって
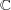 は順序体ではない。
は順序体ではない。