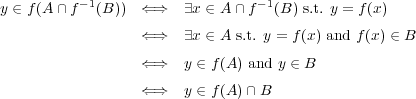距離空間論 演習問題 第2回
-
問題 1.
2つの写像に対し次を示せ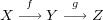
- (a)
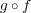 が全射
が全射
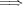
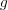 が全射
が全射
- (b)
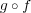 が単射
が単射
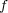 が単射
が単射
解答:
- (a)
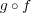 が全射ならば
が全射ならば
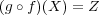 である。ここで
より
である。ここで
より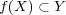 であり
であり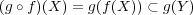 となる。ところが
となる。ところが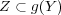
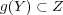 であるから
となる。
であるから
となる。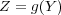
- (b)
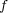 が単射であることを示すために
と仮定する 。両辺を
が単射であることを示すために
と仮定する 。両辺を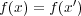
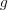 で写して
となるが
で写して
となるが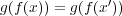
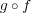 が単射であることより
となる。これで
が単射であることより
となる。これで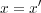
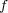 が単射であることが示された。
が単射であることが示された。
- (a)
-
問題 2.
写像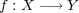 に対し次が成り立つことを確かめよ:
に対し次が成り立つことを確かめよ:
- (a)
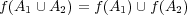 、より一般に
、より一般に
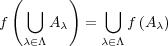
- (b)
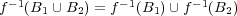 、より一般に
、より一般に
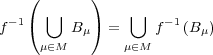
- (c)
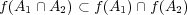 、 より 一 般 に
、 より 一 般 に
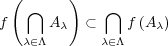
- (d)
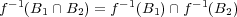 、 より 一 般 に
、 より 一 般 に
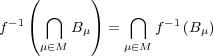
- (e)
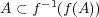
解答:
一般の場合を示す。- (a)
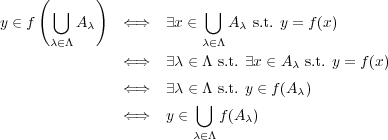
- (b)
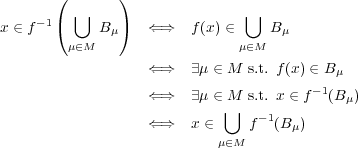
- (c)
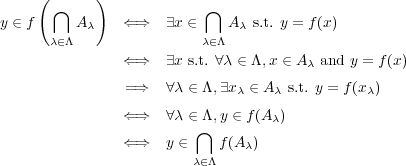
- (d)
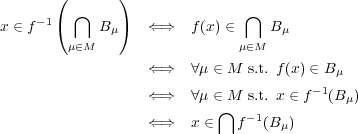
- (e)
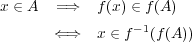
- (a)
-
問題 3.
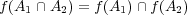 とならない写像
とならない写像
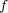 の例を挙げよ。また
の例を挙げよ。また
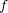 が単射ならば、常に
が単射ならば、常に
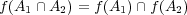 であることを示せ。
であることを示せ。
解答:
基本的に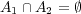 であるが
であるが
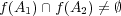 である例を見つければよい。
ほとんどの人が例は有限集合で考えてくれていたが、高校のときによく使った
である例を見つければよい。
ほとんどの人が例は有限集合で考えてくれていたが、高校のときによく使った
 次関数を使うと以下のような例がある:
写像
次関数を使うと以下のような例がある:
写像
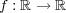 を
を
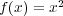 で定義する。
に 対 し
で定義する。
に 対 し![A = [- 2,- 1] 1A2 = [1,2]](img/answers2_45x.gif)
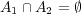 だから
であるが
だから
であるが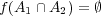 である 。
である 。![f(A1) ∩f(A2) = [1,4]∩ [1,4] = [1,4] ⁄= ∅](img/answers2_48x.gif)
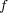 が単射であるときの証明は以下の通り: 問題 2(c)で
が示されているので
が単射であるときの証明は以下の通り: 問題 2(c)で
が示されているので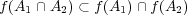 を示せばよい。
を示せばよい。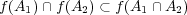 このとき
このとき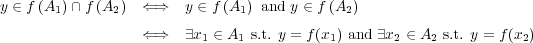 であるから、
であるから、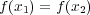
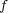 が単射であることより
となる。これを
が単射であることより
となる。これを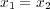
 とおくと 、
とおくと 、
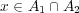 となり
となる。よって
となり
となる。よって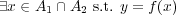 である。
である。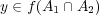
-
問題 4:
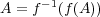 とならない写像
とならない写像
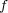 の例を挙げよ。また
の例を挙げよ。また
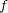 が単射ならば、常に
が単射ならば、常に
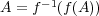 であることを示せ。
であることを示せ。
解答 :
これも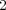 次関数の例を挙げる。問題 3と同じ関数
次関数の例を挙げる。問題 3と同じ関数
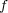 に対し、
に対し、
![A = [0,1]](img/answers2_66x.gif) とおくと
である。
とおくと
である。![f-1([0,1]) = {x ∈ ℝ | x2 ∈ [0,1]} = [- 1,1] ⁄= A](img/answers2_67x.gif)
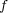 が単射であることの証明は以下の通り: 問題 2(e)より
であることは分っているので
が単射であることの証明は以下の通り: 問題 2(e)より
であることは分っているので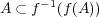 を示せばよい。
を示せばよい。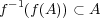 ここで
ここで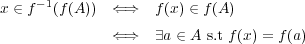
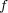 が単射だから
が単射だから
 、よって
、よって
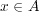 となる。よって
が示された。
となる。よって
が示された。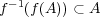
-
問題 5:
写像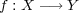 と
と
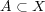 と
と
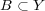 に対し次を示せ :
に対し次を示せ :
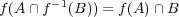
解答 :