距離空間論演習問題 第1回
-
問題 1.
真理表により、集合の和と共通部分について次が成り立つことを確かめよ- (a)
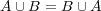
- (b)
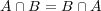
- (c)
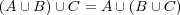
- (d)
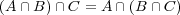
- (e)
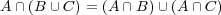
- (f)
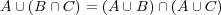
解答:
真理表の書き方はほとんどの人が分かっているようなので、省略。 - (a)
-
問題 2.
集合の差について次が成り立つことを確かめよ- (a)
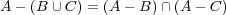
- (b)
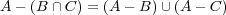
- (c)
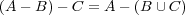
- (d)
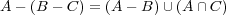
- (e)
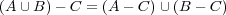
解答:
真理表を使ってもできるが、問題 1. の結果を使うことにする。ド・モルガン (de Morgan) の法則が本質的である。- (a)
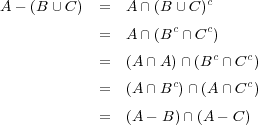
- (b)
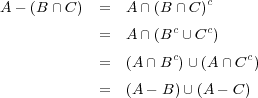
- (c)
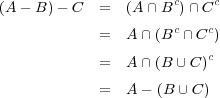
- (d)
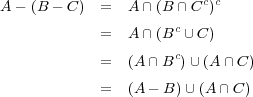
- (e)
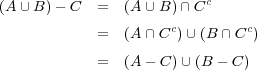
- (a)
-
問題 3.
集合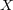 の部分集合
の部分集合
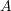 と
と
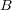 について次を示せ:
について次を示せ:
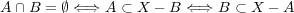
解答:
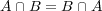 より
を示せばよい。
より
を示せばよい。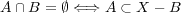 ここで下から二番目の
ここで下から二番目の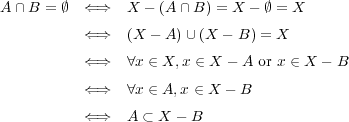
 では次のことを用いた:
では次のことを用いた:
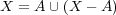 だから
だから
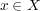 について
について
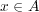 かまたは
かまたは
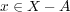 であり、
であり、
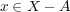 ならば
ならば
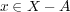 である。
である。
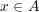 の場合は
の場合は
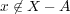 だから
だから
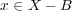 となる。
となる。