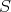 が有限集合である場合、
が有限集合である場合、
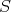 に含まれる要素の数を
に含まれる要素の数を
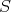 の濃度という。すなわち、既に定義した記号で
の濃度という。すなわち、既に定義した記号で
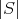 が
が
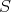 の濃度である。無限集合に対しても濃度を考えよう。前の定義では、無限集合
の濃度である。無限集合に対しても濃度を考えよう。前の定義では、無限集合
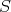 に対してはすべて
に対してはすべて
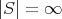 と書いた。すべての無限は同じであろうか。これを考えるために、二つの集合に対して濃度が大きい、小さいという概念を定義する。
と書いた。すべての無限は同じであろうか。これを考えるために、二つの集合に対して濃度が大きい、小さいという概念を定義する。
集合
 が有限集合である場合、
が有限集合である場合、
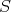 に含まれる要素の数を
に含まれる要素の数を
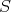 の濃度という。すなわち、既に定義した記号で
の濃度という。すなわち、既に定義した記号で
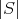 が
が
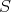 の濃度である。無限集合に対しても濃度を考えよう。前の定義では、無限集合
の濃度である。無限集合に対しても濃度を考えよう。前の定義では、無限集合
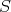 に対してはすべて
に対してはすべて
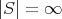 と書いた。すべての無限は同じであろうか。これを考えるために、二つの集合に対して濃度が大きい、小さいという概念を定義する。
と書いた。すべての無限は同じであろうか。これを考えるために、二つの集合に対して濃度が大きい、小さいという概念を定義する。
簡単のために二つの有限集合
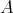 ,
,
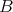 を考える。
を考える。
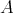 と
と
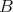 から同時に一つずつ元を取っていき、先に元がなくなった方が濃度は小さいといえる。例えば
から同時に一つずつ元を取っていき、先に元がなくなった方が濃度は小さいといえる。例えば
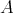 が先になくなったとしよう。このとき
が先になくなったとしよう。このとき
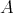 の元
の元
 に対して、
に対して、
 と同時に取った
と同時に取った
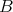 の元
の元
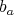 を対応させれば写像
を対応させれば写像
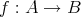 が得られる。また一つの
が得られる。また一つの
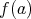 に対して
に対して
 と異なる
と異なる
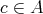 で
で
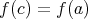 となることはないからこの写像は単射である。一般に単射
となることはないからこの写像は単射である。一般に単射
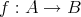 が存在するとき
が存在するとき
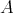 の濃度は
の濃度は
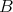 の濃度以下である。これを無限集合に対しても適用する。この節では無限集合
の濃度以下である。これを無限集合に対しても適用する。この節では無限集合
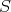 に対して、その濃度を
に対して、その濃度を
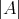 で表すが
で表すが
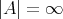 という記号は用いないで、無限を区別することにする。
という記号は用いないで、無限を区別することにする。
定義5.1.1. 二つの集合
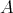 ,
,
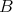 に対して単射
に対して単射
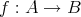 が存在するとき
が存在するとき
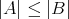 と定義する。また
と定義する。また
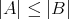 であって
であって
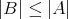 でないとき
でないとき
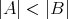 と表す。
と表す。
全単射
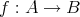 が存在するとき
が存在するとき
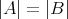 と定義する。
と定義する。
このようなときに集合の濃度が大きい、小さい、等しいなどということにする。
二つの有限集合
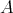 ,
,
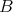 に対して
に対して
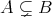 であるならば
であるならば
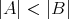 であることは感覚的に理解できるであろう。では無限集合ではどうだろうか。
であることは感覚的に理解できるであろう。では無限集合ではどうだろうか。
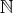 を自然数全体の集合として
を自然数全体の集合として
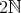 を偶数である自然数全体の集合とする。このとき
を偶数である自然数全体の集合とする。このとき
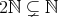 である。しかし写像
である。しかし写像
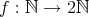 を
を
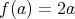 で定めれば、これは全単射である。よって
で定めれば、これは全単射である。よって
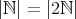 が成り立つ。したがって無限集合に対しては
が成り立つ。したがって無限集合に対しては
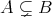 であっても
であっても
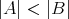 とは限らないことになる。
とは限らないことになる。
証明.
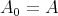 ,
,
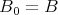 とおいて、帰納的に
とおいて、帰納的に
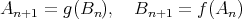
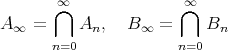
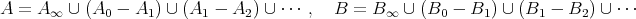
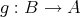 は単射であるから
は単射であるから
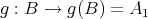 と見ればこれは全単射である。よって
と見ればこれは全単射である。よって
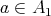 に対して
に対して
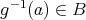 が定義される。
が定義される。
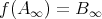 を 示 す。 まず、任意の
を 示 す。 まず、任意の
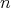 に対して
に対して
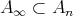 であるから
であるから
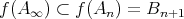 であり、よって
であり、よって
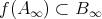 である。また
である。また
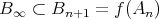 であるから
であるから
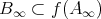 も成り立つ。よって
も成り立つ。よって
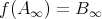 である。
である。
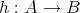 を
を

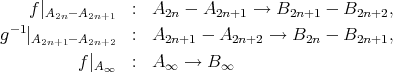
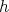 は全単射となる。
は全単射となる。
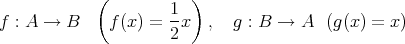
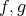 は共に単射であり、よって
は共に単射であり、よって
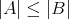 かつ
かつ
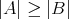 となる。 Bernsteinの定理はこのとき
となる。 Bernsteinの定理はこのとき
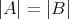 であることを主張している。すなわち、全単射
であることを主張している。すなわち、全単射
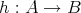 が存在することを意味している。実際にこの全単射を構成してみよう。
が存在することを意味している。実際にこの全単射を構成してみよう。
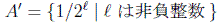 とおく。
とおく。
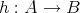 を
を
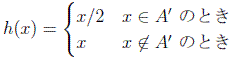
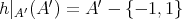 であり、また
であり、また
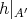 は単射である。また
は単射である。また
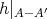 が全単射であることは明らかである。よって
が全単射であることは明らかである。よって
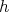 は
は
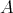 から
から
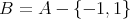 への全単射となる。
への全単射となる。
注意. 全射
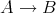 が存在すれば
が存在すれば
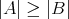 のように思えるが、これは後で紹介する選択公理を用いなければ示すことができない。
のように思えるが、これは後で紹介する選択公理を用いなければ示すことができない。
任意の二つの集合
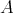 ,
,
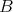 に対して
に対して
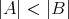 ,
,
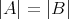 ,
,
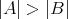 のいずれかが成り立つように思われる。しかしこれも選択公理を用いなければ示すことができない (濃度の比較可能定理)。
のいずれかが成り立つように思われる。しかしこれも選択公理を用いなければ示すことができない (濃度の比較可能定理)。
自然数全体の集合
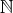 と同じ濃度をもつ集合を可算無限集合という。可算無限集合の濃度を
と同じ濃度をもつ集合を可算無限集合という。可算無限集合の濃度を
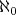 と書きアレフゼロと読む。可算無限集合は無限集合の中で最も小さいものであるといえる。よって
と書きアレフゼロと読む。可算無限集合は無限集合の中で最も小さいものであるといえる。よって
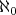 は無限濃度のうちで最も小さいものである。可算無限集合と有限集合を合わせて可算集合という。
は無限濃度のうちで最も小さいものである。可算無限集合と有限集合を合わせて可算集合という。
例5.1.6. 以下の集合はすべて可算無限集合である。「自然数全体の集合
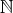 」、「偶数全体の集合」、「奇数全体の集合」、「直積集合
」、「偶数全体の集合」、「奇数全体の集合」、「直積集合
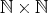 」「整数全体の集合
」「整数全体の集合
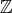 」、「有理数全体の集合
」、「有理数全体の集合
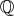 」、「可算無限集合の無限部分集合」
」、「可算無限集合の無限部分集合」
可算集合でない無限集合は存在するのであろうか。以下の命題が可算集合でない無限集合の例を示している。
実数全体の集合
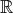 の濃度
の濃度
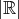 を連続体濃度といい
を連続体濃度といい
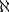 と表す (アレフと読む) 。「
と表す (アレフと読む) 。「
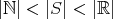 となるような集合
となるような集合
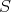 が存在するか 」という問題は連続体仮説などと呼ばれ数学的に証明できないことが証明されている。では無限集合の濃度は他にあるのだろうか。これには明快に答えることができて、無限集合の濃度はいくらでも存在する。
が存在するか 」という問題は連続体仮説などと呼ばれ数学的に証明できないことが証明されている。では無限集合の濃度は他にあるのだろうか。これには明快に答えることができて、無限集合の濃度はいくらでも存在する。
証明.
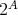 は
は
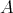 の部分集合全体の集合である。よって元の数が
の部分集合全体の集合である。よって元の数が
 である部分集合全体の集合を考えれば、それと
である部分集合全体の集合を考えれば、それと
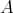 との間に全単射が存在し、よって
との間に全単射が存在し、よって
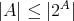 である。
である。
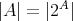 と仮定する。このとき全単射
と仮定する。このとき全単射
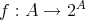 が存在する。
が存在する。
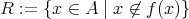
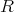 は
は
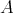 の部分集合なので
の部分集合なので
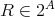 である。
である。
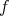 は全単射なので、ある
は全単射なので、ある
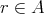 があって
があって
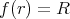 である。ここで
である。ここで
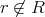 とすると
とすると
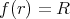 より
より
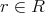 で矛盾。
で矛盾。
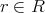 とすると
とすると
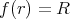 より
より
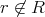 で矛盾。
で矛盾。
よって、このような全単射は存在しない。
これを対角線論法という。
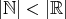 もこれを使って証明される。
もこれを使って証明される。
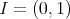 (開区間) として
(開区間) として
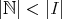 を示そう。例
5.1.3
より
を示そう。例
5.1.3
より
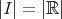 であるから、このことによって
であるから、このことによって
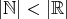 が示される。
が示される。
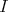 の任意の元
の任意の元
 は
は
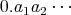 という無限小数として表すことができる。
という無限小数として表すことができる。
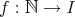 が全単射であるとする。
が全単射であるとする。
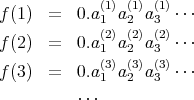
 を少数第
を少数第
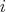 位が
位が
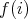 と異なるように作る。そうすれば
と異なるように作る。そうすれば
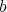 は、どの
は、どの
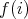 とも異なるので
とも異なるので
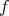 が全単射であることに矛盾する。これが対角線論法と呼ばれる理由も分かって頂けたであろうか。
が全単射であることに矛盾する。これが対角線論法と呼ばれる理由も分かって頂けたであろうか。
さて集合の濃度にはいくらでも大きなものが存在し、濃度が一番大きな集合というものは存在しない。「集合すべての集合」というのが存在するとすれば、それは濃度が一番大きな集合となり、ラッセルのパラドックスと同様に矛盾が生じる。
以下のことは証明なしに結果だけ紹介しておく。 (証明には以下に述べる選択公理を必要とするものもある。)
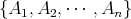 を有限個の空でない集合の族とする。このとき各
を有限個の空でない集合の族とする。このとき各
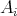 から一つずつ元
から一つずつ元
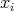 を選ぶことはできる。有限とは限らない集合の族
を選ぶことはできる。有限とは限らない集合の族
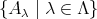 の場合はどうであろうか。実はこれは他の公理からは証明できないことが知られている。しかしこれは感覚的に正しいように思われる。そこで、これを公理として採用し選択公理 (または選出公理) と呼ぶ。
の場合はどうであろうか。実はこれは他の公理からは証明できないことが知られている。しかしこれは感覚的に正しいように思われる。そこで、これを公理として採用し選択公理 (または選出公理) と呼ぶ。
選択公理. 集合の族
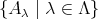 において、どの
において、どの
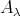 も空でないとする。このとき各
も空でないとする。このとき各
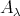 から一つずつ元
から一つずつ元
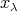 を選ぶことができる。
を選ぶことができる。
これは次のように言い換えることもできる。
選択公理. 集合の族
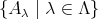 において、どの
において、どの
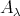 も空でないとする。このとき直積集合
も空でないとする。このとき直積集合
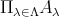 も空でない。
も空でない。
数学の多くの部分で選択公理が利用されているが、選択公理を仮定しない数学もある。 (実は写像のところで既に選択公理を利用しているところがあった。探してみるといいだろう。) 選択公理は以下のツォルンの補題、ツェルメロの整列可能定理と同値であることが知られている。したがって選択公理を仮定している場合には、これらも成り立つとしてよい。
ツォルン(Zorn) の補題. 順序集合
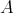 が帰納的ならば
が帰納的ならば
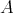 に少なくとも一つの極大元が存在する。
に少なくとも一つの極大元が存在する。
ツェルメロ(Zermelo) の整列可能定理. 任意の集合
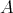 上に整列順序が定義できる。
上に整列順序が定義できる。
整列順序とは、任意の空でない部分集合に最小元が存在する、ということであった。例えば
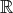 は通常の順序で整列集合ではない。整列可能定理は、うまく順序を入れれば
は通常の順序で整列集合ではない。整列可能定理は、うまく順序を入れれば
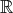 も整列順序にできる、ということを主張している。これは明らかとは言えないだろう。
も整列順序にできる、ということを主張している。これは明らかとは言えないだろう。
以下のことは選択公理を仮定して証明される。
証明. 任意の
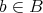 に対して
に対して
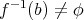 である。各
である。各
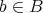 に対して
に対して
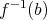 から一つ元を取り、それを
から一つ元を取り、それを
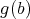 とする (ここで選択公理を使っている)。このとき
とする (ここで選択公理を使っている)。このとき
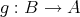 は単射であり
は単射であり
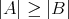 となる。
となる。
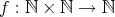 を
を
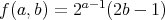 で定めると、これは全単射であること を示せ。
で定めると、これは全単射であること を示せ。
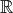 と
と
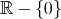 の間の全単射を構成せよ。
の間の全単射を構成せよ。