定義4.1.1 (関係).
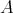 を集合とする。直積集合
を集合とする。直積集合
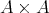 の部分集合
の部分集合
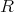 を
を
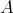 上の二項関係、または単に関係という。
上の二項関係、または単に関係という。
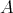 上に関係
上に関係
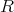 が定められていることを明示したい場合には
が定められていることを明示したい場合には
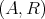 と書く。
と書く。
など、いくら書いてもきりがない。 これは数学的な対象についても同様である。同じ集合に属する二つの元の “関係” について、それを数学的に定義し、議論する。
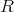 を関係とするとき
を関係とするとき
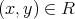 であることを
であることを
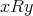 とも書くことにする。
とも書くことにする。
この例において、 (1), (2), (3) では “
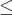 ” などを定義する右辺で “
” などを定義する右辺で “
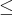 ” 自身を使っていて、好ましい記述ではないが、例を理解するには十分であろう。
” 自身を使っていて、好ましい記述ではないが、例を理解するには十分であろう。
ここに挙げた例は (例
4.1.3
を除いて) よく知られた性質を用いて関係を定義しているが、一般に
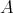 上の関係は
上の関係は
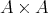 の部分集合と言うだけでよいので、かなり自由に関係を定義できる。
の部分集合と言うだけでよいので、かなり自由に関係を定義できる。
通常の生活でも、順序という言葉はよく用いられる。例えば、小学生でも背の低い順に列に並んだりする。この順序について考えよう。順序を表す記号として、よく使われるものを用いると、いろいろな先入観が入りやすいので、ここでは
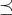 という、あまり使われない記号を用いることにする。
という、あまり使われない記号を用いることにする。
定義4.2.1 (順序関係). 集合
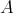 上の関係
上の関係
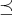 が順序関係、または単に順序であるとは、以下の条件を満たすこととする。
が順序関係、または単に順序であるとは、以下の条件を満たすこととする。
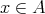 に対して
に対して
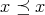
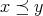 ,
,
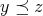 ならば
ならば
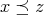
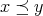 ,
,
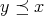 ならば
ならば
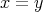
このとき
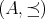 を順序集合という。
を順序集合という。
例4.2.2. 「ジャンケン」を考えよう。「グー」は「チョキ」に強く、「チョキ」は「パー」に強く、「パー」は「グー」に強い。これは推移律が成り立たないことを意味しており、ジャンケンにおける「強い」ということは、関係を定めてはいるが、それは順序関係ではない。
例4.2.3. 例
4.1.2
の
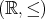 ,
,
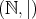 ,
,
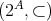 はすべて順序集合である。例
4.1.2
の
はすべて順序集合である。例
4.1.2
の
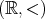 は条件 (1) を満たさないので順序集合ではない。例
4.1.3
は条件 (1) を満たさないので順序集合ではない。例
4.1.3
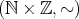 は条件 (3)を満たさないので順序集合ではない。
は条件 (3)を満たさないので順序集合ではない。
練習のため例
4.1.2
の
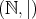 が順序集合であることを示しておこう。
が順序集合であることを示しておこう。
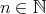 に対して
に対して
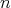 は
は
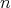 の約数であるから
の約数であるから
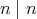 である。
である。
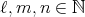 に対して
に対して
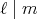 ,
,
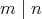 とすると
とすると
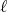 は
は
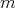 の約数であり
の約数であり
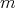 は
は
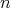 の約数であるから
の約数であるから
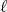 は
は
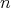 の約数である。したがって
の約数である。したがって
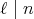 が成り立つ。
が成り立つ。
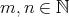 に対して
に対して
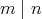 かつ
かつ
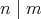 とすると
とすると
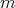 は
は
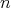 の約数で
の約数で
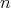 は
は
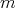 の約数なので
の約数なので
 である。
である。
以上より
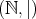 が順序集合であることが示される。
が順序集合であることが示される。
ここで注意したいのは、例えば
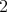 と
と
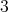 については
については
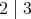 も
も
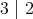 も成り立たないということである。一般に順序集合の任意の二つの要素について「どちらかが大きい」という順序が定まるわけではない。
も成り立たないということである。一般に順序集合の任意の二つの要素について「どちらかが大きい」という順序が定まるわけではない。
定義4.2.4 (全順序). 順序集合
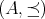 の任意の二つの要素
の任意の二つの要素
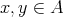 に対して
に対して
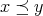 または
または
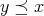 が成り立つとき、この順序を全順序といい、この順序集合を全順序集合という。単なる順序を全順序とはっきり区別したいときには半順序という言い方もする。
が成り立つとき、この順序を全順序といい、この順序集合を全順序集合という。単なる順序を全順序とはっきり区別したいときには半順序という言い方もする。
例4.2.6. 前述の「小学生を背の低い順に並べる」ということを考えよう。ある小学校のクラスの生徒を、ある身体測定の際の身長の小さい順に並べるとする。より一般に、集合
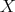 と写像
と写像
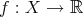 が与えられ、
が与えられ、
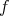 による値によって、集合
による値によって、集合
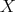 の順序を決めるということを考えよう。自然に考えられる順序
の順序を決めるということを考えよう。自然に考えられる順序
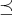 の決め方として
の決め方として
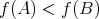 のとき
のとき
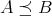 、すなわち
、すなわち
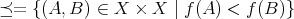
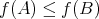 のとき
のとき
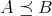 、すなわち
、すなわち
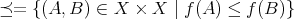
が考えられる。 (1) は推移律、非対称律をみたすが、反射律をみたさないので順序ではない。 (2) は反射律、推移律をみたすが、非対称律をみたさないので、やはり順序ではない。順序を定義するには
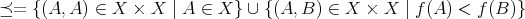
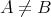 で
で
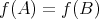 であるものに対しては
であるものに対しては
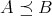 でも
でも
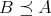 でもなく、よってこの順序は全順序ではない。
でもなく、よってこの順序は全順序ではない。
順序集合
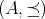 を考える。
を考える。
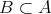 に対して
に対して
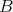 の順序を
の順序を
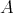 の順序で定めれば、
の順序で定めれば、
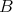 はまた順序集合になる。これを順序部分集合と呼ぶ。
はまた順序集合になる。これを順序部分集合と呼ぶ。
順序集合
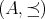 の元
の元
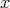 に対して
に対して
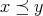 ならば
ならば
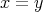 が成り立つとき
が成り立つとき
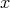 を
を
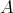 の極大元という。同様に
の極大元という。同様に
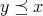 ならば
ならば
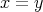 であるとき
であるとき
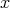 を
を
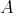 の極小元という。任意の
の極小元という。任意の
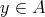 に対して
に対して
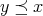 のとき
のとき
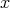 を
を
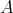 の最大元という。任意の
の最大元という。任意の
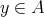 に対して
に対して
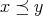 のとき
のとき
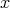 を
を
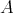 の最小元という。最大元は極大元、最小元は極小元であるが、逆は成り立つとは限らない。最大元、最小元は存在するとは限らないが、存在すれば唯一つに定まる。
の最小元という。最大元は極大元、最小元は極小元であるが、逆は成り立つとは限らない。最大元、最小元は存在するとは限らないが、存在すれば唯一つに定まる。
例4.2.7. 例
4.1.2
の順序集合
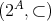 を考える。
を考える。
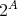 には最大元
には最大元
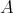 と最小元
と最小元
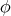 が存在する。
が存在する。
例4.2.8. 例
4.1.2
の順序集合
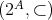 を考え、その順序部分集合
を考え、その順序部分集合
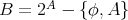 を考える。ここで
を考える。ここで
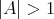 と仮定する。このとき
と仮定する。このとき
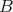 には最大元も最小元も存在しない。任意の
には最大元も最小元も存在しない。任意の
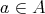 に対して
に対して
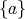 は
は
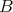 の極小元であり、
の極小元であり、
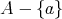 は
は
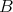 の極大元である。
の極大元である。
証明. 極大元についてのみ示せば、極小元についても同様である。
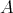 を全順序集合とし
を全順序集合とし
 をその極大元とする。
をその極大元とする。
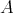 が全順序集合なので、任意の
が全順序集合なので、任意の
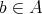 に対して
に対して
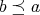 または
または
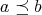 が成り立つが、
が成り立つが、
 が極大であることから
が極大であることから
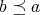 である。よって
である。よって
 は最大元である。 _
は最大元である。 _
順序集合
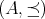 の部分集合
の部分集合
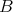 に対して
に対して
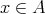 が
が
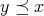 (
(
 ) を満たすとき、
) を満たすとき、
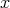 を
を
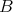 の上界という。
の上界という。
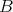 の上界が存在するとき
の上界が存在するとき
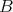 は上に有界であるという。
は上に有界であるという。
証明.
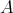 を全順序集合ではない順序集合とする。このとき
を全順序集合ではない順序集合とする。このとき
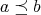 でも
でも
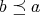 でもない
でもない
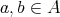 が存在する。例
4.2.14
と同じように
が存在する。例
4.2.14
と同じように
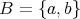 を考えれば
を考えれば
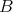 には最小元は存在しない。 _
には最小元は存在しない。 _
![B = [a ,a ,⋅⋅⋅] 1 2](img/set1705x.gif) を順序集合
を順序集合
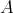 の元の列とする。 (同じ元を含んでもよい。よって
の元の列とする。 (同じ元を含んでもよい。よって
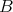 は部分集合ということではないので異なる記号を用いている。)
は部分集合ということではないので異なる記号を用いている。)
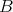 が単調減少列 (単調増加列) であるとは
が単調減少列 (単調増加列) であるとは
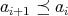 (
(
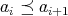 ) が任意の
) が任意の
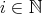 について成り立つこととする。また
について成り立つこととする。また
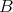 が狭義単調減少列 (狭義単調増加列) であるとは減少列 (増加列) であって
が狭義単調減少列 (狭義単調増加列) であるとは減少列 (増加列) であって
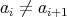 が任意の
が任意の
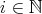 について成り立つこととする。
について成り立つこととする。
証明. 整列集合
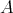 に無限の狭義単調減少列
に無限の狭義単調減少列
![B = [a1,a2,⋅⋅⋅]](img/set1716x.gif) が存在したとする。このとき
が存在したとする。このとき
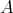 の部分集合
の部分集合
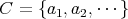 を考える。
を考える。
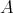 が整列集合だから
が整列集合だから
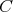 には最小元が存在する。
には最小元が存在する。
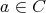 を
を
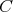 の最小元とする。
の最小元とする。
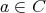 だから、ある
だから、ある
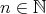 があって
があって
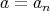 である。しかし
である。しかし
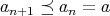 ,
,
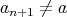 となり、
となり、
 が最小元であることに矛盾する。よって
が最小元であることに矛盾する。よって
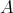 に無限の狭義単調減少列は存在しない。 _
に無限の狭義単調減少列は存在しない。 _
例4.2.17 (辞書式順序).
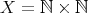 に次のように順序を定める。
に次のように順序を定める。
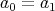 ならば
ならば
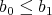 のとき
のとき
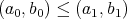 である。
である。
 のとき
のとき
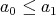 ならば
ならば
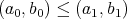 である。
である。
この順序は整列順序である。これを辞書式順序という。
やや分かりにくいと思うので具体的に書くと以下のようになる。
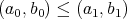 かつ
かつ
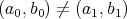 であることを簡単のために
であることを簡単のために
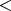 とかく。
とかく。
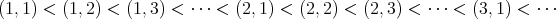
これが整列順序であることを示そう。
 を
を
 の空でない部分集合とする。
の空でない部分集合とする。
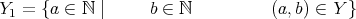
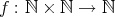 を
を
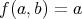 で定めて
で定めて
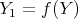 としているのである。
としているのである。
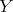 が空でないから
が空でないから
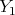 も空でない。
も空でない。
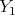 は
は
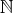 の部分集合で、
の部分集合で、
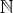 は整列集合なので
は整列集合なので
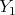 には最小元
には最小元
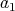 が存在する。
が存在する。
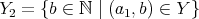
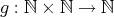 を
を
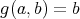 で定めて
で定めて
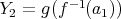 としているのである。
としているのである。
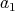 の決め方から
の決め方から
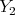 は空でない
は空でない
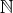 の部分集合で、したがって
の部分集合で、したがって
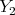 は最小元
は最小元
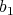 をもつ。このとき
をもつ。このとき
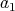 ,
,
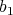 の決め方から
の決め方から
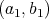 は
は
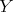 の最小元である。
の最小元である。
例4.2.18. 例
4.2.17
で
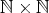 に辞書式順序を定めたが、これは次のように一般化される。
に辞書式順序を定めたが、これは次のように一般化される。
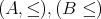 をそれぞれ整列順序とする。このとき例
4.2.17
と同様に
をそれぞれ整列順序とする。このとき例
4.2.17
と同様に
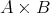 に順序を定めれば、これも整列順序となる。この順序も辞書式順序と呼ばれる。これによって
に順序を定めれば、これも整列順序となる。この順序も辞書式順序と呼ばれる。これによって
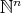 なども辞書式順序で整列集合と見ることができる。
なども辞書式順序で整列集合と見ることができる。
証明. 最大元は任意の部分集合の上界であるから、任意の部分集合は上に有界である。 _
数学的帰納法の通常の形は以下の通りである。
自然数
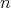 に関する命題は
に関する命題は
 のとき正しい。
のとき正しい。
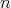 より小さいすべての自然数に対して正しければ
より小さいすべての自然数に対して正しければ
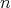 についても正しい。
についても正しい。
が成り立てば、任意の
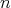 に対しても正しい。 (2) は
に対しても正しい。 (2) は
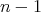 に対して正しければ
に対して正しければ
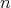 についても正しい。
についても正しい。
という形で考えられることもある。
これは整列集合に一般化される。すなわち
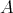 を整列集合とするとき
を整列集合とするとき
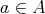 に関する命題は
に関する命題は
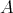 の最小元に対して正しい。
の最小元に対して正しい。
 より小さいすべて元に対して正しければ
より小さいすべて元に対して正しければ
 についても正し い。
についても正し い。
が成り立つとき、任意の
 に対しても正しい。これは整列集合には無限の狭義単調減少列が存在しないことによる。すなわち
に対しても正しい。これは整列集合には無限の狭義単調減少列が存在しないことによる。すなわち
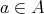 を決めると、狭義単調減少列は有限回で最小元に達する。したがって命題は有限回の手続きで証明されることになる。数学的帰納法を整列集合に一般化したものを超限帰納法という。
を決めると、狭義単調減少列は有限回で最小元に達する。したがって命題は有限回の手続きで証明されることになる。数学的帰納法を整列集合に一般化したものを超限帰納法という。
考える順序集合が整列集合ではない場合、例えば通常の順序を考えた実数体
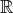 など、では数学的帰納法や超限帰納法は使えない。以下の論法は正しくない。
など、では数学的帰納法や超限帰納法は使えない。以下の論法は正しくない。
しかし、例えば以下の論法は正しい。
数学においては (数学以外でもそうであると思うが) 色々な意味で「同じである」という概念を用いる。例えば分数
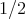 と
と
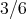 は同じ数であるが、明らかにその表記は異なる。他にも例えば合同な二つの三角形はある意味では「同じ」と言える。しかし、同じと言う概念をあまり勝手に使うと感覚的に理解しがたいことになる。同値関係は「同じ」という概念を数学的に定式化したものと考えられる。主張していることは
は同じ数であるが、明らかにその表記は異なる。他にも例えば合同な二つの三角形はある意味では「同じ」と言える。しかし、同じと言う概念をあまり勝手に使うと感覚的に理解しがたいことになる。同値関係は「同じ」という概念を数学的に定式化したものと考えられる。主張していることは
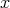 と
と
 が「同じ」ならば
が「同じ」ならば
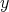 と
と
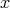 も「同じ」である。
も「同じ」である。
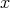 と
と
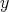 が「同じ」で
が「同じ」で
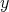 と
と
 が「同じ」ならば
が「同じ」ならば
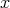 と
と
 は「同じ」である。
は「同じ」である。
という当たり前のことである。これが成り立たない場合に「同じ」という言葉を使うのが感覚的に受け入れがたいということも理解できるだろう。
例4.4.2. 例
4.1.3
,
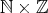 上の関係
上の関係
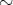 は同値関係である。これを示そう。
は同値関係である。これを示そう。
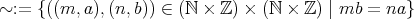
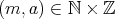 に対して
に対して
 は成立するので
は成立するので
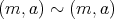 で ある。
で ある。
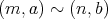 とすると
とすると
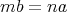 であるから
であるから
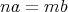 である。よって
である。よって
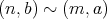 である。
である。
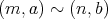 ,
,
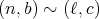 とする。このとき
とする。このとき
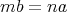 ,
,
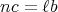 であ る。よって
であ る。よって
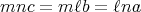 である。ここで
である。ここで
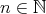 より
より
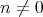 なので
なので
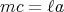 が成り立ち
が成り立ち
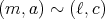 である。
である。
以上より
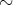 は同値関係である。
は同値関係である。
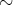 を集合
を集合
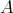 上の同値関係とする。
上の同値関係とする。
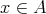 に対して
に対して
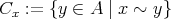
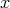 を含む (
を含む (
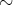 に関する) 同値類と呼ぶ。すなわち
に関する) 同値類と呼ぶ。すなわち
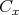 は
は
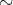 に関して
に関して
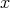 と「同じ」もの全体の集合である。このとき次が成り立つ。
と「同じ」もの全体の集合である。このとき次が成り立つ。
証明. (1) は反射律より明らか。
(2)
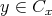 と仮定する。定義より
と仮定する。定義より
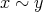 である。また対称律より
である。また対称律より
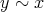 である。
である。
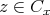 とする。このとき
とする。このとき
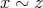 である。よって
である。よって
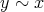 ,
,
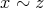 となり、推移律より
となり、推移律より
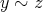 であり
であり
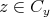 である。したがって
である。したがって
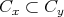 である。
である。
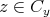 とする。このとき
とする。このとき
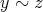 である。
である。
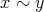 ,
,
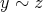 であるから推移律により
であるから推移律により
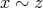 である。よって
である。よって
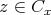 であり
であり
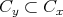 が成り立つ。
が成り立つ。
以上より
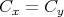 である。
である。
(3)
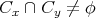 なので
なので
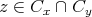 とする。このとき
とする。このとき
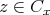 なので (2) より
なので (2) より
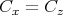 であり、同様に
であり、同様に
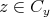 より
より
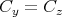 である。よって
である。よって
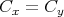 である。
である。
(4) は (3) の対偶である。 _
定理
4.4.3
より
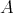 の異なる同値類の全体を
の異なる同値類の全体を
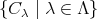 とおくと
とおくと
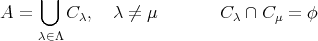
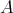 の同値関係
の同値関係
 による類別という。各同値類
による類別という。各同値類
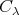 から一つずつ元
から一つずつ元
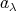 を選ぶとき
を選ぶとき
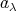 を
を
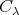 の代表元という。また集合
の代表元という。また集合
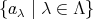 をこの類別の完全代表系という。
をこの類別の完全代表系という。
例4.4.4. 例
4.1.3
の同値関係
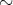 は実はよく知られたものである。それは
は実はよく知られたものである。それは
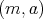 を有理数
を有理数
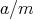 に対応させると分かる。
に対応させると分かる。
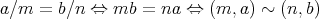
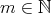 となっているので分母が
となっているので分母が
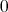 にならないことにも注意しておく。
にならないことにも注意しておく。
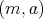 を含む同値類は分数として
を含む同値類は分数として
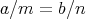 となる
となる
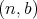 の全体である。すなわち
の全体である。すなわち
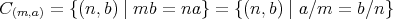
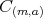 の代表元として、例えば
の代表元として、例えば
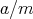 が既約分数であるものを取ることができる。ただし
が既約分数であるものを取ることができる。ただし
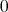 の既約分数表示は
の既約分数表示は
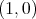 としておく。したがって既約分数の全体がこの同値関係による類別の完全代表系である。
としておく。したがって既約分数の全体がこの同値関係による類別の完全代表系である。
注意. 一般に同値類の代表元の取り方は一意的ではない。この例では既約分数を代表元に取ったが、他の代表元をとっても構わず、その場合には完全代表系も違うものになる。
例
4.4.4
をもう少し考える。
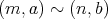 であるとき、有理数としては
であるとき、有理数としては
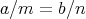 であるが
であるが
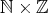 では
では
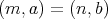 という訳ではない。写像
という訳ではない。写像
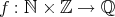 (
(
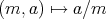 ) を定めることは出来るがこれは全単射ではない。同値類全体の集合
) を定めることは出来るがこれは全単射ではない。同値類全体の集合
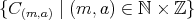 を考えれば写像
を考えれば写像
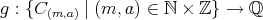 (
(
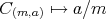 ) は矛盾なく定義でき (well-defined) かつ全単射であることを示そう。
) は矛盾なく定義でき (well-defined) かつ全単射であることを示そう。
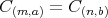 であるならば
であるならば
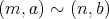 であるから
であるから
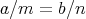 である。したがって
である。したがって
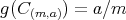 は定まり、写像は矛盾なく定義できる。
は定まり、写像は矛盾なく定義できる。
任意の有理数
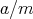 (
(
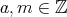 ,
,
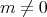 ) に対して、
) に対して、
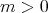 ならば
ならば
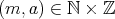 で
で
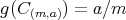 である。また
である。また
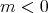 ならば
ならば
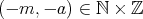 で
で
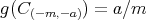 である。よって
である。よって
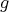 は全射である。
は全射である。
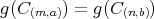 とすると
とすると
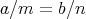 であるから
であるから
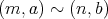 であり
であり
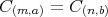 が成り立つ。よって
が成り立つ。よって
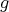 は単射である。
は単射である。
以上より
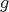 は矛盾なく定義でき、かつ全単射であることが示された。
は矛盾なく定義でき、かつ全単射であることが示された。
この例では
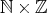 自身は
自身は
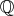 との間に全単射がないが、その同値類の全体は
との間に全単射がないが、その同値類の全体は
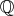 との間に全単射がある。すなわち一つの同値類を一つのものと見ることが有効である。これは数学では多く見られる方法である。一般に集合
との間に全単射がある。すなわち一つの同値類を一つのものと見ることが有効である。これは数学では多く見られる方法である。一般に集合
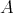 の上に同値関係
の上に同値関係
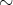 が定義されているとき、その同値類全体の集合を
が定義されているとき、その同値類全体の集合を
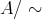 と書き、集合
と書き、集合
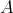 を同値関係
を同値関係
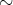 で割った集合という。先の例では
で割った集合という。先の例では
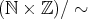 と
と
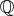 の間に全単射があったのである。
の間に全単射があったのである。
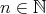 を一つ固定する。
を一つ固定する。
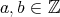 に対して
に対して
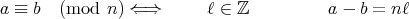
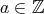 に対して、この関係による
に対して、この関係による
 を含む同値類は
を含む同値類は
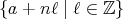 と書くことができる。これを
と書くことができる。これを
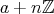 と書き
と書き
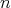 を法とする
を法とする
 を含む剰余類という。特に
を含む剰余類という。特に
 は単に
は単に
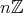 と書かれる。任意の剰余類
と書かれる。任意の剰余類
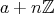 に対して、その代表元
に対して、その代表元
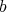 を
を
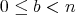 の範囲で取ることができることは明らかだろう。また
の範囲で取ることができることは明らかだろう。また
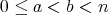 ならば
ならば
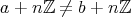 であることも明らかである。したがって
であることも明らかである。したがって
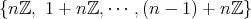 が同値類のすべてである。この集合を
が同値類のすべてである。この集合を
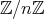 と書く。
と書く。
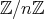 に二項演算 “
に二項演算 “
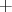 ” を次のように定義しよう。
” を次のように定義しよう。
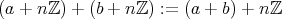
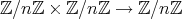 であるから、これが矛盾なく定義されていることを示そう。
であるから、これが矛盾なく定義されていることを示そう。
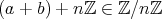 は問題ないが、演算が代表元の取り方に依存しないことを示す必要がある。すなわち
は問題ないが、演算が代表元の取り方に依存しないことを示す必要がある。すなわち
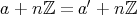 ,
,
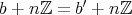 であるときに
であるときに
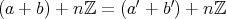 でなければならない。
でなければならない。
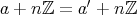 ,
,
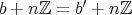 と仮定する。これは、ある
と仮定する。これは、ある
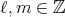 があって
があって
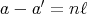 ,
,
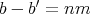 と書けるということである。このとき
と書けるということである。このとき
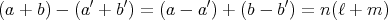
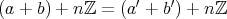 である。よって、この演算は矛盾なく定義できる。
である。よって、この演算は矛盾なく定義できる。
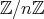 に二項演算 “
に二項演算 “
 ” を
” を
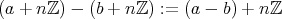 で矛盾なく定義 できることを示せ。
で矛盾なく定義 できることを示せ。
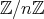 に二項演算 “
に二項演算 “
 ” を
” を
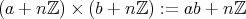 で矛盾なく定義でき ることを示せ。
で矛盾なく定義でき ることを示せ。
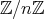 の加法と乗法は交換法則、結合法則を満たすことを示せ。ま た減法は一般には交換法則、結合法則を満たさないことを示せ。
の加法と乗法は交換法則、結合法則を満たすことを示せ。ま た減法は一般には交換法則、結合法則を満たさないことを示せ。
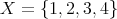 とする。
とする。
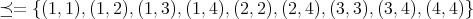 は
は
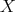 上の 順序関係であることを確認せよ。この順序は全順序かどうかを判定せよ。また 最大元、最小元、極大元、極小元をそれぞれ求めよ。
上の 順序関係であることを確認せよ。この順序は全順序かどうかを判定せよ。また 最大元、最小元、極大元、極小元をそれぞれ求めよ。
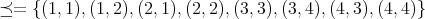 は
は
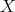 上の同値関 係であることを確認せよ。またこの同値関係による類別を求めよ。
上の同値関 係であることを確認せよ。またこの同値関係による類別を求めよ。
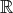 の元を成分に持つ
の元を成分に持つ
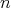 次正方行列の全体を
次正方行列の全体を
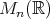 と書く。
と書く。
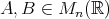 に対し て、関係
に対し て、関係
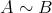 を「ある正則行列
を「ある正則行列
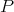 があって
があって
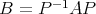 となる」ということで定 義する。このとき
となる」ということで定 義する。このとき
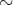 は同値関係であることを示せ。
は同値関係であることを示せ。
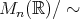 を考える。
を考える。
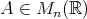 を含む同値類を
を含む同値類を
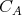 と書くことにする。このとき
と書くことにする。このとき
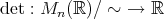 (
(
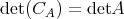 ) が矛盾なく 定義できることを説明せよ。ただし
) が矛盾なく 定義できることを説明せよ。ただし
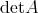 は
は
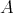 の行列式である。
の行列式である。
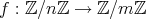 を
を
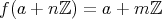 で定義したい。
で定義したい。
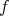 が矛盾なく定義される ための必要十分条件を求めよ。
が矛盾なく定義される ための必要十分条件を求めよ。
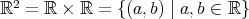 を考え、
を考え、
 とする。
とする。
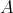 に
に
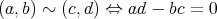
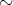 を定める。
を定める。
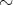 は同値関係であり、その同値類の完全代表系として座標平面 上の単位円 (半径
は同値関係であり、その同値類の完全代表系として座標平面 上の単位円 (半径
 の円) 上の点
の円) 上の点
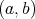 のうち
のうち
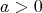 であるもの、および
であるもの、および
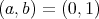 からなる集合をとることができる。これを示せ。 (この同値類全体の集合を
からなる集合をとることができる。これを示せ。 (この同値類全体の集合を
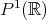 と書いて射影空間という。)
と書いて射影空間という。)