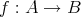
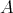 ,
,
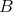 を集合とする。
を集合とする。
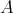 の各元に対して
の各元に対して
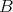 の元が一つ定まっているとする。このときこの対応を
の元が一つ定まっているとする。このときこの対応を
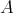 から
から
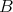 への写像という。
への写像という。
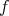 が
が
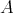 から
から
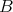 への写像であることを
への写像であることを
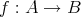
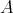 を定義域、
を定義域、
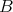 を値域という。写像
を値域という。写像
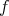 によって
によって
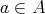 に対応する
に対応する
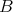 の元を
の元を
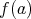 と表し、これを
と表し、これを
 の
の
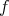 による像という。どのように定まる写像なのかを明示したい場合には
による像という。どのように定まる写像なのかを明示したい場合には

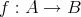 と書けば
と書けば
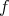 が写像であることを意味するが、以下の例では簡単のため写像ではないものに対しても同様の記号を用いる。
が写像であることを意味するが、以下の例では簡単のため写像ではないものに対しても同様の記号を用いる。
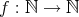 を
を
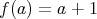 で定めれば、これは写像である。
で定めれば、これは写像である。
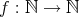 を
を
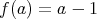 で定めると、これは写像ではない。なぜならば
で定めると、これは写像ではない。なぜならば
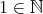 に対して
に対して
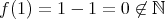 であり、
であり、
 の
の
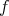 による像が定まらない からである。
による像が定まらない からである。
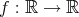 を
を
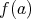 は
は
 の平方根とすると、これは写像ではない。まず正の数 について平方根は
の平方根とすると、これは写像ではない。まず正の数 について平方根は
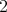 つあり、このどちらを対応させるのかが定かでない。また負 の数については平方根は
つあり、このどちらを対応させるのかが定かでない。また負 の数については平方根は
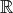 に存在しないので対応が決まらない。
に存在しないので対応が決まらない。
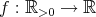 を
を
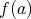 は
は
 の正の平方根とする (すなわち
の正の平方根とする (すなわち
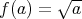 ) と、こ れは写像である。またこのとき値域を
) と、こ れは写像である。またこのとき値域を
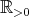 としても、これは写像である。
としても、これは写像である。
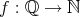 を
を
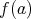 は
は
 の分母として定めると、これは写像ではない。なぜな らば有理数の書き方は一意的でなく、分母の定義が曖昧だからである。これを「分 母が正である既約分数に表したときの分母」とすれば、これは一意的に定まるので 写像になる。ただし「整数に対しては分母を
の分母として定めると、これは写像ではない。なぜな らば有理数の書き方は一意的でなく、分母の定義が曖昧だからである。これを「分 母が正である既約分数に表したときの分母」とすれば、これは一意的に定まるので 写像になる。ただし「整数に対しては分母を
 とする」などの注意も書き加えた 方がよいだろう。
とする」などの注意も書き加えた 方がよいだろう。
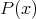 を実数係数多項式とする。このとき
を実数係数多項式とする。このとき
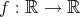 を
を
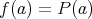 で定めれ ば、これは写像である。通常はこの写像
で定めれ ば、これは写像である。通常はこの写像
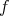 と多項式
と多項式
 に同じ記号を用いる。
に同じ記号を用いる。
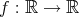 ,
,
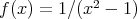 は
は
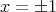 で値が定まらないので写像ではな い。
で値が定まらないので写像ではな い。
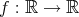 ,
,
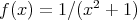 は写像である。
は写像である。
この例を見れば分かるように写像
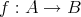 が定まるためには次のことが必要である。
が定まるためには次のことが必要である。
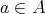 に対して
に対して
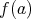 が定まる。ただし
が定まる。ただし
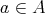 の記述の仕方が一意的で ない場合には、どのような記述に対しても同じ元が対応しなければならない。
の記述の仕方が一意的で ない場合には、どのような記述に対しても同じ元が対応しなければならない。
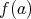 は
は
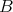 の元である。
の元である。
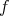 がこの条件を満たすとき
がこの条件を満たすとき
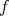 が定まる、または
が定まる、または
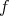 は矛盾なく定義される(well-defined) という。
は矛盾なく定義される(well-defined) という。
二つの写像
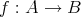 と
と
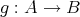 が等しいとは、任意の
が等しいとは、任意の
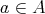 に対して
に対して
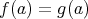 となることとする。
となることとする。
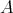 を空でない任意の集合とする。
を空でない任意の集合とする。
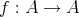 を、任意の
を、任意の
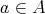 に対して
に対して
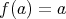 とすれば
とすれば
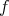 は写像である。これを
は写像である。これを
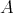 の恒等写像といい
の恒等写像といい
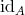 と書く。 (
と書く。 (
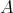 が空のときも恒等写像は定義できるが、その意味は分かりにくいだろう。)
が空のときも恒等写像は定義できるが、その意味は分かりにくいだろう。)
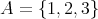 ,
,
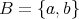 と す る。
と す る。
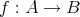 を
を
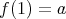 ,
,
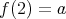 ,
,
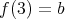 で定めればこれは写像である。写像
で定めればこれは写像である。写像
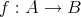 を決めるには
を決めるには
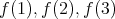 を任意に定めればよいので
を任意に定めればよいので
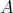 から
から
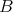 への写像は全部で
への写像は全部で
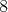 個あることが分かる。
個あることが分かる。
より一般に
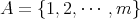 ,
,
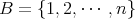 とするとき
とするとき
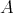 から
から
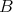 への写像は
への写像は
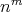 個ある。 (
個ある。 (
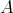 から
から
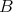 への写像全体の集合を
への写像全体の集合を
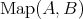 , または
, または
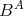 などと書いたりする。)
などと書いたりする。)
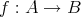 ,
,
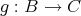 をそれぞれ写像とする。このとき
をそれぞれ写像とする。このとき
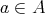 を
を
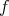 で移して、続けて
で移して、続けて
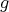 で移すという操作が考えられる。このように考えると
で移すという操作が考えられる。このように考えると
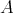 から
から
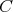 への新しい写像が得られる。これを
への新しい写像が得られる。これを
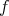 と
と
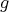 の合成写像といい
の合成写像といい
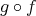 と書く。
と書く。

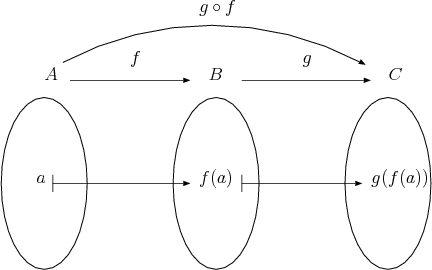
|
Figure3.1: 
|
はじめに
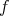 で移しているのに
で移しているのに
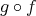 と書くのは、その像が
と書くのは、その像が
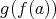 となっているからである。 (場合によっては写像の合成を逆の順序で書くこともあるが、この講義ではこの順序で統一する。) このとき
となっているからである。 (場合によっては写像の合成を逆の順序で書くこともあるが、この講義ではこの順序で統一する。) このとき
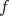 の値域と
の値域と
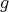 の定義域が一致していることが重要で、そうでないときには合成写像は考えられない。 (実際には
の定義域が一致していることが重要で、そうでないときには合成写像は考えられない。 (実際には
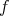 の値域が
の値域が
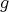 の定義域に含まれていればよいが、正確には後で説明する。)
の定義域に含まれていればよいが、正確には後で説明する。)
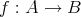 を考える。また
を考える。また
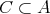 とする。
とする。
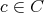 は
は
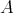 の元でもあるので
の元でもあるので
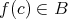 が定まる。このようにして写像
が定まる。このようにして写像
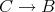 が定義される。これを
が定義される。これを
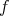 の
の
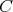 への制限、または制限写像といい
への制限、または制限写像といい
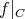 と書く。
と書く。
これと似たこととして
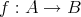 に対して、すべての像
に対して、すべての像
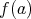 が
が
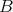 の部分集合
の部分集合
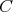 に含まれるならば、自然に
に含まれるならば、自然に
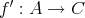 (
(
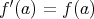 ) が定義できる。 (
) が定義できる。 (
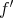 は同じ記号
は同じ記号
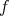 を用いて表されることも多い。)
を用いて表されることも多い。)
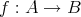 を考える。
を考える。
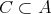 に対して
に対して
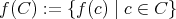
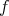 による
による
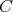 の像という。定義から明らかなように
の像という。定義から明らかなように
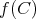 は
は
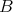 の部分集合である。
の部分集合である。
ここで注意するのは
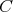 は
は
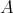 の部分集合であって
の部分集合であって
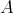 の元ではないので、今までの意味では
の元ではないので、今までの意味では
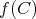 は定義されない。この場合の
は定義されない。この場合の
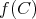 とは新しく定義した記号であり、通常の意味での写像の像ではない。
とは新しく定義した記号であり、通常の意味での写像の像ではない。
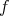 に対して
に対して
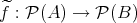 を
を
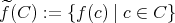 で定めると、これは写像である。
で定めると、これは写像である。
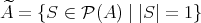 とおくと、
とおくと、
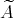 は自然に
は自然に
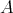 と同じものと考えることができる。同様に
と同じものと考えることができる。同様に
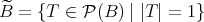 とおくと、
とおくと、
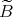 は自然に
は自然に
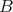 と同じものと考えることができる。このように考えれば、制限写像
と同じものと考えることができる。このように考えれば、制限写像
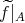 は
は
 と同じものと考えられる。この意味で
と同じものと考えられる。この意味で
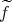 を
を
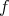 と書けば、上で説明したような記号となる。
と書けば、上で説明したような記号となる。
特に
 としたとき
としたとき
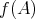 を単に
を単に
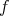 の像といい
の像といい
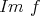 とも書く。
とも書く。
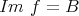 が成り立つとき
が成り立つとき
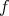 を全射という。すなわち
を全射という。すなわち
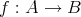 が全射であるとは
が全射であるとは
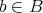 に対して、ある
に対して、ある
 があって
があって
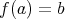 となる
となる
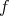 が全射であることを
が全射であることを
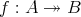 などと書くこともある。
などと書くこともある。
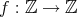 (
(
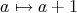 ) は全射である。なぜならば、任意の
) は全射である。なぜならば、任意の
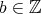 に対して
に対して
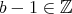 であり
であり
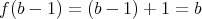 が成り立つからである。
が成り立つからである。
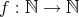 (
(
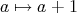 ) は全射ではない。なぜならば、
) は全射ではない。なぜならば、
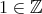 に対して
に対して
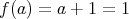 となる
となる
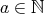 が存在しないからである (そのような
が存在しないからである (そのような
 は
は
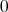 であるが
であるが
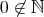 である)。
である)。
証明.
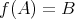 ,
,
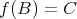 であるから
であるから
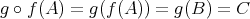 である。 _
である。 _
証明.
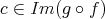 とする。このとき、ある
とする。このとき、ある
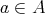 があって
があって
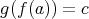 である。
である。
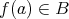 であるから
であるから
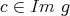 である。よってはじめの主張を得る。
である。よってはじめの主張を得る。
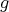 が全射でなければ
が全射でなければ
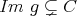 であり
であり
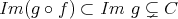 となるから
となるから
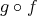 は全射ではない。 _
は全射ではない。 _
証明.
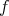 が全射であるとし、
が全射であるとし、
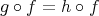 とする。
とする。
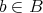 を任意にとる。
を任意にとる。
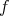 は全射なので、ある
は全射なので、ある
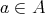 があって
があって
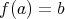 である。このとき
である。このとき
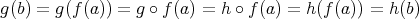
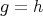 である。
である。
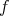 が全射でないとする。
が全射でないとする。
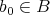 で
で
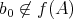 なるものが存在する。
なるものが存在する。
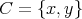 (
(
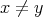 ) とおき、任意の
) とおき、任意の
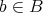 に対して
に対して
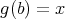 で
で
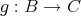 を定め、
を定め、
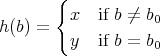
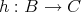 を定める。このとき
を定める。このとき
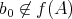 としているので、任意の
としているので、任意の
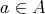 に対して
に対して
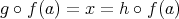 となる。すなわち
となる。すなわち
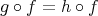 であるが
であるが
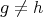 なので、
なので、
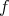 は命題の条件を満たさない。 _
は命題の条件を満たさない。 _
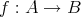 を考える。
を考える。
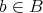 に対して
に対して
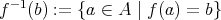
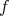 による
による
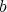 の逆像という。これも単なる記号であり
の逆像という。これも単なる記号であり
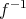 は写像ではない。 (正確には
は写像ではない。 (正確には
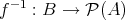 である。)
である。)
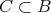 に対しても
に対しても
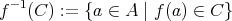
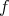 による
による
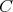 の逆像という。 (この場合、正確には
の逆像という。 (この場合、正確には
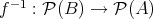 である。)
である。)
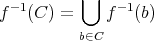
任意の
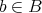 に対して
に対して
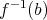 が高々一つの元しか含まないとき、
が高々一つの元しか含まないとき、
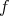 を単射という。言い換えると
を単射という。言い換えると
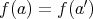 ならば
ならば
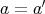 である
である
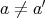 ならば
ならば
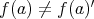 である (上の命題の対偶)
である (上の命題の対偶)
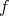 が単射であることを
が単射であることを
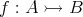 などと書くこともある。
などと書くこともある。
証明.
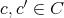 に対して
に対して
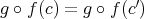 とする。
とする。
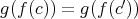 で
で
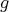 が単射なので
が単射なので
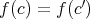 である。また
である。また
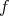 が単射なので
が単射なので
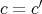 である。よって
である。よって
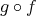 は単射である。 _
は単射である。 _
証明.
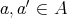 とし
とし
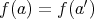 とする。このとき
とする。このとき
 である。
である。
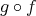 が単射であるから
が単射であるから
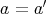 である。よって
である。よって
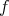 は単射である。 _
は単射である。 _
証明.
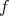 が 単 射 で あ る と し、
が 単 射 で あ る と し、
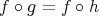 と する。
と する。
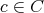 に対して
に対して
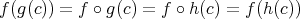 である。
である。
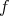 が単射なので
が単射なので
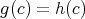 となり
となり
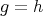 となる。
となる。
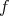 が単射でないとする。
が単射でないとする。
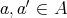 ,
,
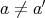 で
で
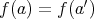 となるものがある。
となるものがある。
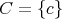 とおいて
とおいて
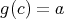 ,
,
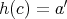 として
として
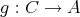 ,
,
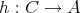 を定める。このとき
を定める。このとき
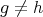 であるが
であるが
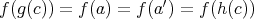 となり
となり
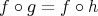 が成り立つ。よって命題の条件はみたされない。 _
が成り立つ。よって命題の条件はみたされない。 _
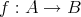 が全単射であるとは、
が全単射であるとは、
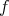 が全射かつ単射であることとする。言い換えると
が全射かつ単射であることとする。言い換えると
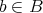 に対して
に対して
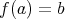 となる
となる
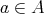 が唯一つ存在する
が唯一つ存在する
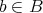 に対して
に対して
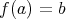 となる
となる
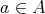 が存在する」ことから全射、「唯一つ存在する」ということから単射であることが分かる。この言い換えから全単射
が存在する」ことから全射、「唯一つ存在する」ということから単射であることが分かる。この言い換えから全単射
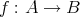 に対しては、
に対しては、
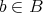 に対して
に対して
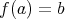 となる
となる
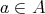 を対応させることによって写像
を対応させることによって写像
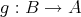 が定まる。この写像
が定まる。この写像
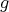 を
を
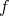 の逆写像といって
の逆写像といって
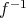 で表す。逆像の定義でも
で表す。逆像の定義でも
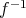 という記号を用いたが、そのときは
という記号を用いたが、そのときは
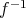 は単なる記号であった。しかしここでは
は単なる記号であった。しかしここでは
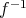 は写像であるので注意が必要である。
は写像であるので注意が必要である。
証明.
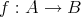 が全単射であれば
が全単射であれば
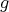 として
として
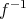 をとれば命題
3.6.2
より
をとれば命題
3.6.2
より
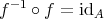 ,
,
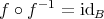 は共に全単射である。
は共に全単射である。
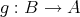 に対して
に対して
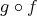 ,
,
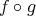 が共に全単射であるとする。このとき
が共に全単射であるとする。このとき
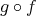 が全射であるから命題
3.4.4
より
が全射であるから命題
3.4.4
より
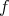 は全射であり、
は全射であり、
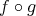 が単射であるから命題
3.5.6
より
が単射であるから命題
3.5.6
より
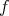 は単射である。 _
は単射である。 _
証明のために簡単な補題を用意しよう。補題の証明は定義から明らかである。
定理
3.6.4
の証明. (3)
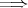 (1), (3)
(1), (3)
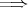 (2) は明らか。 (1)
(2) は明らか。 (1)
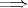 (2),(2)
(2),(2)
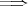 (1) を示せばよい。
(1) を示せばよい。
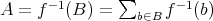 であり、
であり、
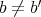 ならば
ならば
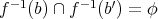 なので
なので
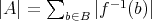 であることに注意しておく。
であることに注意しておく。
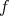 を単射とする。
を単射とする。
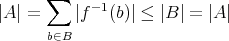
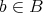 に対して
に対して
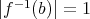 である。よって
である。よって
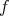 は全射である。
は全射である。
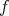 を全射とする。
を全射とする。
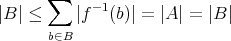
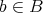 に対して
に対して
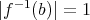 である。よって
である。よって
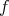 は単射である。 _
は単射である。 _
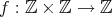 に他ならない。
に他ならない。
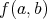 を
を
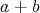 という記号を用いて表しているだけである。
という記号を用いて表しているだけである。
このように、ある集合
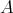 に対して、写像
に対して、写像
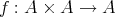 が与えられるとき、それを
が与えられるとき、それを
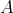 の二項演算という。二項演算の像は適当な記号、ここでは仮に
の二項演算という。二項演算の像は適当な記号、ここでは仮に
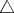 とする、を用いて
とする、を用いて
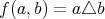 のように表される。二項演算
のように表される。二項演算
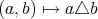 に対して
に対して

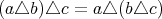
このとき次が成り立つ。
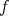 が単射ならば
が単射ならば
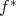 は全射である。
は全射である。
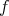 が全射ならば
が全射ならば
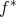 は単射である。
は単射である。
証明. (1)
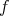 を単射とする。このとき全単射
を単射とする。このとき全単射
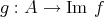 が得られる。任意の
が得られる。任意の
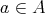 に対して
に対して
 である。
である。
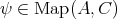 を任意にとる。
を任意にとる。
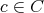 を一つ固定しておく (
を一つ固定しておく (
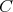 が空集合でないことは仮定している)。
が空集合でないことは仮定している)。
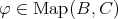 を
を
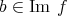 に対しては
に対しては
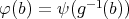 で定め、
で定め、
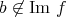 に対しては
に対しては
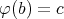 と定める。このとき、任意の
と定める。このとき、任意の
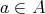 に対して
に対して
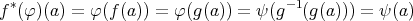
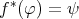 であり、
であり、
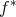 は全射である。
は全射である。
(2)
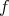 を全射とする。
を全射とする。
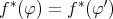 とする。このとき、任意の
とする。このとき、任意の
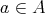 に対して
に対して
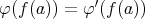 である。
である。
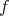 が全射なので
が全射なので
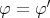 となり
となり
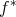 は単射である。 _
は単射である。 _
証明. (1)
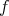 を単射とする。
を単射とする。
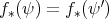 とすれば、任意の
とすれば、任意の
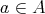 に対して
に対して
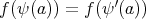 であるが、
であるが、
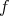 が単射なので
が単射なので
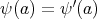 である。よって
である。よって
 であり
であり
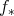 は単射である。
は単射である。
(2)
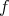 を全射とする。任意の
を全射とする。任意の
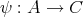 に対して
に対して
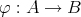 を以下のように定める。
を以下のように定める。
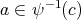 (
(
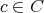 ) ならば
) ならば
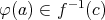 となるようにする。
となるようにする。
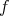 が全射だから、これは可能である。また
が全射だから、これは可能である。また
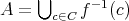 なので、これで任意の
なので、これで任意の
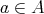 の行き先が定まる (実はここで後で説明する選択公理を使っている)。このようにすれば
の行き先が定まる (実はここで後で説明する選択公理を使っている)。このようにすれば
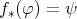 であり
であり
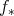 は全射である。 _
は全射である。 _
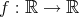 で
で
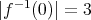 となるものを一つ構成せよ。
となるものを一つ構成せよ。
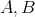 は集合
は集合
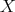 の部分集合、
の部分集合、
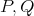 は集合
は集合
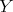 の部分集合とする。写像
の部分集合とする。写像
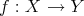 に対して次を示せ。
に対して次を示せ。
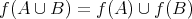
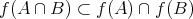 (等しくならない例も作れ)
(等しくならない例も作れ)
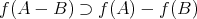 (等しくならない例も作れ)
(等しくならない例も作れ)
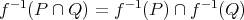
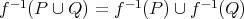
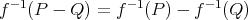
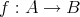 ,
,
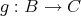 とする。
とする。
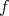 が全単射であるとき、
が全単射であるとき、
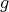 が単射であることと
が単射であることと
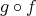 が単射であることは同値である。また
が単射であることは同値である。また
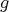 が全射であることと
が全射であることと
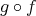 が全射である ことは同値である。以上のことを示せ。
が全射である ことは同値である。以上のことを示せ。
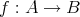 ,
,
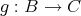 とする。
とする。
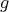 が全単射であるとき、
が全単射であるとき、
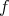 が単射であることと
が単射であることと
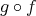 が単射であることは同値である。また
が単射であることは同値である。また
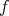 が全射であることと
が全射であることと
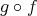 が全射である ことは同値である。以上のことを示せ。
が全射である ことは同値である。以上のことを示せ。
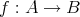 ,
,
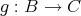 ,
,
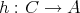 に対して
に対して
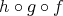 ,
,
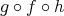 ,
,
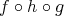 のう ち二つが全射で、残りの一つが単射であるとすると、
のう ち二つが全射で、残りの一つが単射であるとすると、
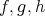 はすべて全単射であることを 示せ。また、二つが単射で、残りの一つが全射であるとしても、
はすべて全単射であることを 示せ。また、二つが単射で、残りの一つが全射であるとしても、
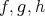 はすべて全単射で あることを示せ。
はすべて全単射で あることを示せ。