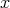 に関する命題
に関する命題
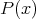 が真となるような
が真となるような
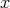 の集まり」という形で記述される。このとき、その集合を
の集まり」という形で記述される。このとき、その集合を
集合とはものの集まりのことである。しかしものの集まりをすべて集合と呼ぶわけではない。
例えば「大きい数の集まり」、「お金持ちの集まり」などはその基準が明確でなく、集合とは言えない。
あるものが集合に属するかどうかははっきりとしていなくてはいけないので、その基準は命題である。よって集合は「
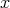 に関する命題
に関する命題
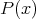 が真となるような
が真となるような
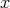 の集まり」という形で記述される。このとき、その集合を
の集まり」という形で記述される。このとき、その集合を
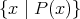
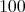 以上の整数の集まり」であれば
以上の整数の集まり」であれば
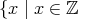 かつ
かつ
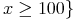
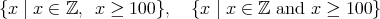
集合
 に属するもの
に属するもの
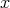 を、その集合の要素、または元という。またこのとき
を、その集合の要素、または元という。またこのとき

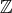 ,
,
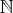 などに用いていたものである。
などに用いていたものである。
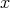 が
が
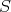 の要素でないことを
の要素でないことを

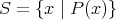 であるとき
であるとき
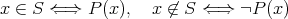
集合の要素を列挙することによって集合を定義することもできる。この場合、要素が
 であれば
であれば
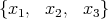
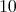 以下の素数全体の集合」は
以下の素数全体の集合」は
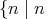 は素数
は素数
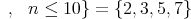
 から
から
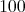 までの整数全体の集合」は
までの整数全体の集合」は
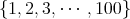
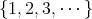
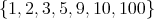 などという集合を
などという集合を
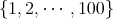 などと書いても誰も理解してくれないであろう。意味が分かりにくい場合や間違える恐れのある場合には省略はしない方がよい。
などと書いても誰も理解してくれないであろう。意味が分かりにくい場合や間違える恐れのある場合には省略はしない方がよい。
集合をこのように要素を並べて表す場合、要素を並べる順番には意味がない。また同じ要素を複数書いても、それは無視される。これは、集合を考えるときには「あるものがその集合に属するか、属さないか」のみが問題とされるからである。例えば次の集合はすべて同じものとして扱われる。

二つの集合
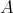 ,
,
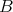 に対して「
に対して「
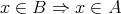 」が成り立つとき
」が成り立つとき
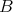 を
を
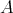 の部分集合といい
の部分集合といい
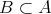 または
または
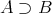 と書く。
と書く。
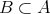 であり、かつある
であり、かつある
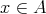 があって
があって
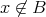 であるとき
であるとき
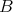 を
を
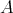 の真部分集合といい
の真部分集合といい
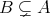 または
または
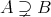 と書く。
と書く。
注意. 部分集合であることを
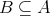 ,
,
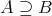 で表し、真部分集合であることを
で表し、真部分集合であることを
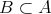 ,
,
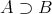 と表す場合もある。講義などで分かりにくい場合は質問をして確認するといいだろう。
と表す場合もある。講義などで分かりにくい場合は質問をして確認するといいだろう。
証明.
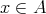 とすると
とすると
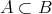 より
より
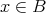 である。また
である。また
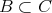 より
より
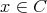 である。よって
である。よって
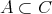 である。 _
である。 _
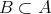 かつ
かつ
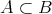 である場合、「
である場合、「
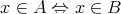 」である。このとき二つの集合
」である。このとき二つの集合
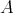 と
と
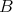 は等しいといい、
は等しいといい、
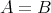 と書く。
と書く。
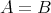 のとき、二つの集合
のとき、二つの集合
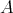 ,
,
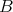 は全く同じ要素からなる。
は全く同じ要素からなる。
前に「
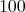 以上の整数の集合」を
以上の整数の集合」を
 と表したが、はじめから
と表したが、はじめから
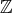 の部分集合を考えているということを意識する場合は
の部分集合を考えているということを意識する場合は
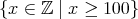
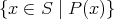
 の部分集合として考えられているということと理解すればよい。
の部分集合として考えられているということと理解すればよい。
集合に含まれる要素の数が有限である場合、その集合を有限集合といい、要素の数が無限であるとき、その集合を無限集合という。有限集合
 の要素の数を
の要素の数を
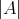 や
や
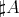 などと書く。無限集合の場合は
などと書く。無限集合の場合は
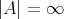 と書く。
と書く。
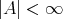 と書かれた場合は
と書かれた場合は
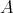 が有限集合であることを意味する。有限集合の部分集合は明らかに有限集合である。有限、無限の定義はやや難しくなるのでここではしない。感覚的に理解しておけば十分である。
が有限集合であることを意味する。有限集合の部分集合は明らかに有限集合である。有限、無限の定義はやや難しくなるのでここではしない。感覚的に理解しておけば十分である。
学習のポイント. 「二つの集合
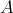 ,
,
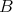 について
について
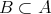 であることを示せ」という問題を考えよう。試験などでこのような問題ができない場合、何を示せばよいのかが分かっていない場合が多く見られる。「
であることを示せ」という問題を考えよう。試験などでこのような問題ができない場合、何を示せばよいのかが分かっていない場合が多く見られる。「
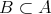 」の定義は「
」の定義は「
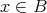 ならば
ならば
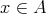 」であるから、証明は以下のようになる。
」であるから、証明は以下のようになる。
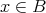 とする。このとき
とする。このとき
 。よって
。よって
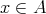 である。したがって
である。したがって
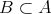 で ある。
で ある。
分かってしまえば簡単なことであるが、きちんと理解しておこう。また「二つの集合
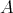 ,
,
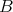 について
について
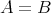 であることを示せ」という問題は、「
であることを示せ」という問題は、「
 」の定義が「
」の定義が「
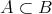 かつ
かつ
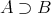 」であるから、
」であるから、
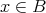 とする。このとき
とする。このとき
 。よって
。よって
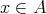 である。したがって
である。したがって
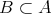 で ある。次に
で ある。次に
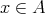 とする。このとき
とする。このとき
 。よって
。よって
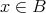 である。したがって
である。したがって
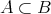 である。以上より
である。以上より
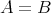 である。
である。
となる。この証明は
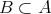 を示す部分と
を示す部分と
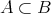 を示す部分からなり、その両方で同じ文字
を示す部分からなり、その両方で同じ文字
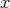 を用いたが、それはまったく違うものである。区別がしにくいと感じるならば、後半では
を用いたが、それはまったく違うものである。区別がしにくいと感じるならば、後半では
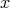 ではなく
ではなく
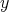 を用いるなどして、紛らわしさがないようにした方がよい。しかし、このような用い方はよくされることなので、ここではあえて同じ記号を用いた。証明などの中で、新しい文字 (記号) を用いるときには、
を用いるなどして、紛らわしさがないようにした方がよい。しかし、このような用い方はよくされることなので、ここではあえて同じ記号を用いた。証明などの中で、新しい文字 (記号) を用いるときには、
などを気にしなければならない。
証明. 「
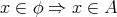 」を示せばよいが
」を示せばよいが
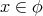 は常に偽であるから、これは常に真である。 _
は常に偽であるから、これは常に真である。 _
証明.
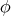 ,
,
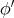 を共に空集合とすると補題
2.2.2
より
を共に空集合とすると補題
2.2.2
より
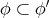 ,
,
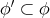 であるから
であるから
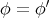 である。 _
である。 _
集合の共通部分について次が成り立つ。
証明. (1), (2) は定義より明らか。
(3)
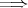 を示す。
を示す。
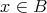 ならば
ならば
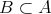 より
より
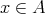 なので
なので
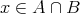 である。よって
である。よって
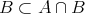 である。また (1) より
である。また (1) より
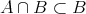 である。以上より
である。以上より
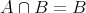 である。
である。
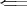 を示す。
を示す。
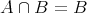 とすると (1) より
とすると (1) より
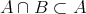 なので
なので
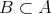 である。 _
である。 _
証明. (1)
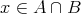 とすると定理
2.3.3
(1) より
とすると定理
2.3.3
(1) より
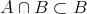 なので
なので
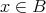 である。同様に
である。同様に
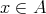 であり、よって
であり、よって
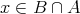 である。したがって
である。したがって
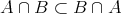 である。逆も同様に示される。
である。逆も同様に示される。
(2)
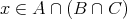 とする。
とする。
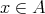 である。
である。
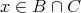 であるから
であるから
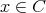 かつ
かつ
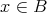 である。以上より
である。以上より
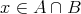 かつ
かつ
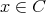 が成り立ち
が成り立ち
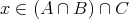 である。よって
である。よって
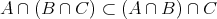 である。逆も同様に示される。 _
である。逆も同様に示される。 _
この定理の (1) を
 の交換法則といい (2) を
の交換法則といい (2) を
 の結合法則という。この二つの性質により三つ以上の集合の共通部分を考えるとき、カッコをつけなくてもその意味は不明にはならない。以後
の結合法則という。この二つの性質により三つ以上の集合の共通部分を考えるとき、カッコをつけなくてもその意味は不明にはならない。以後
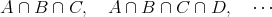
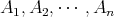 に対して
に対して
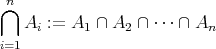
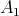 ,
,
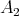 ,
,
 ,
,
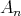 ,
,
 に対して
に対して
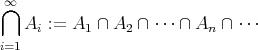
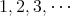 のようになっていなくてもよい。例えば集合
のようになっていなくてもよい。例えば集合
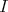 を添字にもつ集合の族
を添字にもつ集合の族
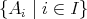 に対しても、その共通部分を
に対しても、その共通部分を
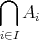
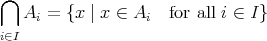
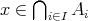 を示したければ、任意の
を示したければ、任意の
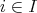 に対して
に対して
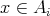 を示せばよい。
を示せばよい。
例2.3.5.
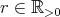 に対して、閉区間
に対して、閉区間
![Ir := [- r,r]](img/set631x.gif) を考える。このとき
を考える。このとき
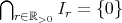 である。
である。
二つの集合が等しいことを示すので、これを示すには
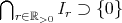 と
と
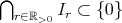 を示すことになる。まず任意の
を示すことになる。まず任意の
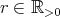 に対して
に対して
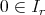 は明らかなので
は明らかなので
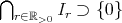 である。
である。
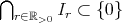 を示すには「
を示すには「
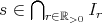 ならば
ならば
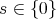 (すなわち
(すなわち
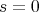 )」を示せばよい。このためにこれの対偶「
)」を示せばよい。このためにこれの対偶「
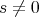 ならば
ならば
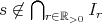 」を示す。
」を示す。
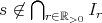 であることと、ある
であることと、ある
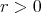 があって
があって
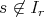 であることは同値である。したがって「
であることは同値である。したがって「
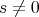 ならば、ある
ならば、ある
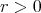 があって
があって
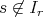 」を示せばよい。。
」を示せばよい。。
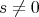 とする。このとき明らかに
とする。このとき明らかに
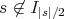 である。
である。
注意.
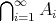 の定義は
の定義は
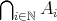 であって
であって
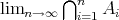 ではない。なぜならば、この極限は定義されていない。
ではない。なぜならば、この極限は定義されていない。
和集合について次が成り立つ。
証明. (1) は明らか。 (2) を示す。
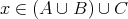 ならば
ならば
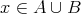 または
または
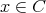 である。まず
である。まず
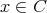 とすると
とすると
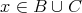 なので
なので
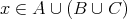 である。また
である。また
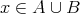 とすると
とすると
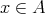 または
または
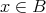 である。
である。
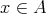 ならば
ならば
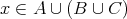 である。
である。
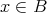 ならば
ならば
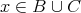 なので
なので
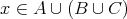 である。以上より、どの場合にも
である。以上より、どの場合にも
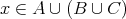 となり
となり
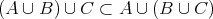 である。逆も同様にして示すことができる。 _
である。逆も同様にして示すことができる。 _
この定理の (1) を
 の交換法則といい (2) を
の交換法則といい (2) を
 の結合法則という。この二つの性質により三つ以上の集合の和集合を考えるとき、カッコをつけなくてもその意味は不明にはならない。以後
の結合法則という。この二つの性質により三つ以上の集合の和集合を考えるとき、カッコをつけなくてもその意味は不明にはならない。以後
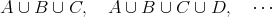
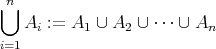
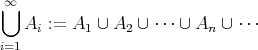
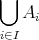
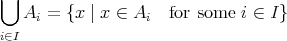
明らかに次が成り立つ。
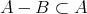
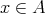 ならば
ならば
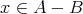 または
または
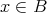
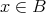 ならば
ならば
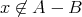
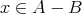 ならば
ならば
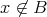
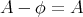 ,
,
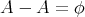
証明.
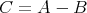 とおく。
とおく。
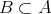 とする。
とする。
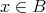 であるならば
であるならば
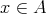 であるから
であるから
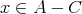 または
または
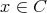 である。しかし
である。しかし
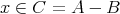 とすると
とすると
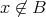 となり矛盾である。よって
となり矛盾である。よって
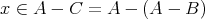 となり
となり
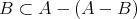 である。逆に
である。逆に
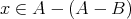 とする。
とする。
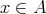 かつ
かつ
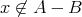 である。よって
である。よって
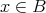 である。したがって
である。したがって
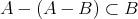 が成り立ち、以上より
が成り立ち、以上より
 である。
である。
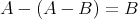 とする。このとき
とする。このとき
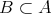 は明らかである。 _
は明らかである。 _
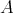 を
を
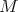 の部分集合とするとき、明らかに次が成り立つ。
の部分集合とするとき、明らかに次が成り立つ。
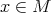 ならば
ならば
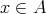 または
または
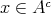
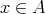 ならば
ならば
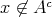
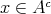 ならば
ならば
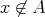
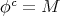 ,
,
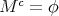
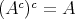
証明. (1)
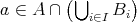 とする。
とする。
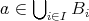 なので、ある
なので、ある
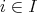 があって
があって
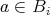 である。よって
である。よって
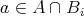 となり
となり
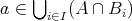 である。
である。
逆に
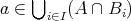 とする。ある
とする。ある
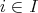 があって
があって
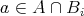 である。よって
である。よって
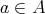 かつ
かつ
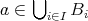 となり
となり
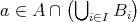 である。
である。
(2)
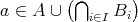 とする。
とする。
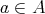 ならば、 任意の
ならば、 任意の
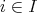 について
について
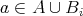 だから
だから
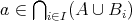 である。また
である。また
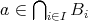 とすると、任意の
とすると、任意の
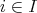 について
について
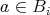 だから
だから
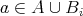 となる。よって、このときも
となる。よって、このときも
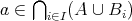 である。
である。
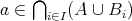 とする。
とする。
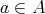 ならば
ならば
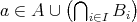 である。
である。
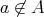 とする。このとき、任意の
とする。このとき、任意の
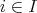 に対して
に対して
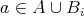 より
より
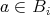 である。よって
である。よって
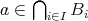 となり
となり
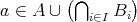 である。
である。
(3)
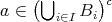 とする。このとき任意の
とする。このとき任意の
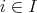 に対して
に対して
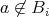 であるから
であるから
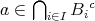 である。
である。
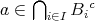 とする。任意の
とする。任意の
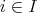 に対して
に対して
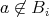 なので
なので
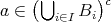 である。
である。
(4) は (3) とほぼ同じに示される。 _
二つのもの
 と
と
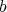 を並べたもの
を並べたもの
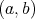 を
を
 と
と
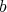 から作られた順序対という。順序対
から作られた順序対という。順序対
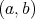 と
と
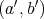 が等しいことを
が等しいことを
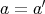 かつ
かつ
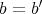 で定め、このとき
で定め、このとき
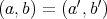 と書く。
と書く。
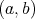 と
と
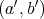 が等しくないことは
が等しくないことは
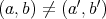 と書く。明らかに
と書く。明らかに
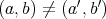 であることと
であることと
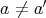 または
または
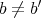 が成り立つことは同値である。
が成り立つことは同値である。
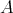 ,
,
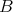 を集合とする。
を集合とする。
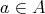 と
と
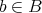 とから作られた順序対
とから作られた順序対
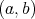 の全体からなる集合を
の全体からなる集合を
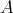 と
と
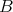 の直積、または直積集合と呼び
の直積、または直積集合と呼び
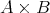 で表す。
で表す。
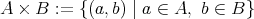
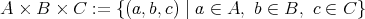
注意.
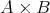 と
と
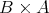 は違うものと考えなくてはならない。
は違うものと考えなくてはならない。
一般に同じ集合いくつかの直積を次のように表す。
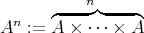
有限とは限らない集合の族
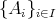 に対しても、その直積集合は定義できる。これを
に対しても、その直積集合は定義できる。これを
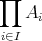
注意. 集合の族
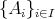 に対して、任意の
に対して、任意の
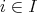 に対して
に対して
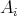 が空でないならば、直積集合
が空でないならば、直積集合
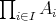 も空でないように思われる。しかしこれは後で述べる選択公理に関することであり、自明ではない。
も空でないように思われる。しかしこれは後で述べる選択公理に関することであり、自明ではない。
集合
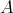 の部分集合すべての集合を
の部分集合すべての集合を
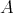 のべき集合 (power set) といい
のべき集合 (power set) といい
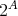 , または
, または
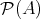 と表す。
と表す。
集合
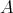 が有限集合である場合には、それぞれの要素が部分集合に含まれるか含まれないかを決めれば部分集合が定まる。したがって
が有限集合である場合には、それぞれの要素が部分集合に含まれるか含まれないかを決めれば部分集合が定まる。したがって
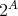 の要素の数は
の要素の数は
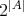 個あることが分かる。これがべき集合を
個あることが分かる。これがべき集合を
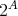 と書く理由である。
と書く理由である。
先に述べたように、ここでは厳密な集合の定義はしていない。しかし集合のようなものの集まりでも集合ではないものが存在することに注意しておく。簡単に言えば、あまりにも大きな集まりは集合ではない場合がある。例えば「集合すべての集まり」は実は集合ではない。これに似た状況から矛盾が生じる「ラッセルのパラドックス」について説明をする。
まず空集合
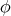 は何も要素を含まないので
は何も要素を含まないので
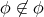 である。このように自分自身を要素として含まない集合すべての集まり
である。このように自分自身を要素として含まない集合すべての集まり
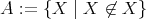 を考える。
を考える。
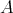 が集合であるとする。
が集合であるとする。
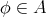 であるから
であるから
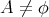 である。
である。
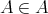 か
か
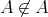 のいずれか一方のみが真である。
のいずれか一方のみが真である。
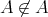 と仮定する。このとき
と仮定する。このとき
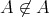 であるから
であるから
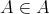 である。これは矛盾で ある。
である。これは矛盾で ある。
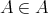 と仮定する。このとき
と仮定する。このとき
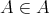 であるから
であるから
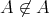 である。これは矛盾で ある。
である。これは矛盾で ある。
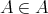 でも
でも
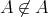 でもあり得ない。これはおかしい。
でもあり得ない。これはおかしい。
これを「ラッセルのパラドックス」という。この場合
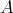 が集合であるとした部分がおかしく、
が集合であるとした部分がおかしく、
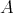 は集合ではない。現在の数学ではこのような矛盾の起きないように集合論を構築しているが、その内容はやや難しい。ここで注意しておくことは
は集合ではない。現在の数学ではこのような矛盾の起きないように集合論を構築しているが、その内容はやや難しい。ここで注意しておくことは
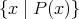 という形で定義されたものでも集合とは限らないと言うことである。
という形で定義されたものでも集合とは限らないと言うことである。
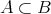 とするとき次を示せ。
とするとき次を示せ。
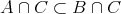
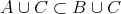
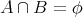 ならば
ならば
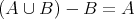 であることを示せ。
であることを示せ。
 かつ
かつ
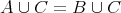 ならば
ならば
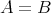 であることを示せ。
であることを示せ。
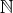 で添字付けられた集合の族
で添字付けられた集合の族
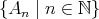 に対して
に対して
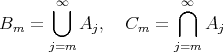
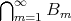 は無数に多くの
は無数に多くの
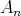 に含まれる元の全体である。
に含まれる元の全体である。
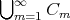 はある番号以上のすべての
はある番号以上のすべての
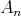 に含まれる元の全体である。
に含まれる元の全体である。
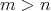 ならば
ならば
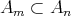 であるとする。このとき
であるとする。このとき
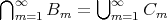 であることを示せ。
であることを示せ。