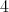 は偶数である。
は偶数である。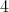 の倍数である。
の倍数である。ここでは数学を学ぶ上で最も基本的である論理学の基本について学ぶ。多くのことは既に知っていることであると思うが、それらを確認しておくということは大事である。勉強をしていて、何かが分からないときには、自分が何を理解していないのかを考えてみると良い。多くの場合、理解できていないのはそのとき勉強していることではなく、もっと前に段階にある。そして、それが実はここで学ぶ論理の部分であるということも少なくはないのである。
それが真 (true) であるか偽 (false) であるかがはっきりとしている事柄を命題という。例えば以下は命題の例である。
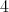 は偶数である。
は偶数である。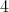 の倍数である。
の倍数である。
もちろん (1), (3) は真で (2), (4) は偽である。 (2) にはやや注意が必要である。偶数のうちには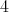 の倍数も含まれているので (2) は真であったり、偽であったりするように思われる。しかし、実は (2) は
の倍数も含まれているので (2) は真であったり、偽であったりするように思われる。しかし、実は (2) は
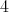 の倍数である。
の倍数である。
ということを主張していると理解されるのである。したがって一つでも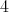 の倍数でない偶数 (例えば
の倍数でない偶数 (例えば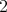 ) があれば偽であるということになるのである。
) があれば偽であるということになるのである。
以下は命題ではない例である。
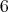 は良い数である。
は良い数である。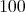 は大きな数である。
は大きな数である。どれも明確な基準が定められておらず、真か偽か判定できない。
自然数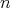 に対して
に対して
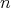 は偶数である。
は偶数である。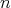 は
は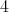 の倍数である。
の倍数である。
とすると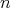 を定めれば
を定めれば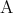 ,
, 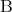 共に真か偽かが定まり、これらは命題である。真であるか偽であるかが
共に真か偽かが定まり、これらは命題である。真であるか偽であるかが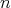 に依存するので、このような場合は単に
に依存するので、このような場合は単に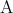 ,
, 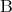 とは書かずに
とは書かずに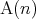 ,
, 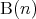 などと書くこともある。
などと書くこともある。
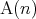 ならば
ならば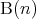 である (偶数は
である (偶数は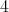 の倍数である)。
の倍数である)。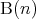 ならば
ならば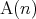 である (
である (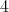 の倍数は偶数である)。
の倍数は偶数である)。
とおくと、これらも命題であり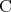 は偽、
は偽、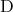 は真である。
は真である。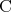 や
や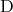 は
は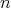 には依存しない命題である。ここで
には依存しない命題である。ここで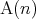 や
や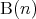 は命題であり「
は命題であり「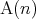 ならば
ならば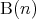 である」というのも命題であることに注意する。
である」というのも命題であることに注意する。
一般に「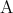 ならば
ならば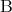 である」ということを
である」ということを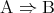 または
または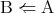 と書く。命題
と書く。命題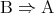 を命題
を命題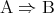 の逆命題、または単に逆という。ある命題が真であっても、その逆が真であるとは限らない。命題
の逆命題、または単に逆という。ある命題が真であっても、その逆が真であるとは限らない。命題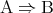 が真であるとき
が真であるとき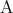 を
を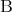 の十分条件といい、
の十分条件といい、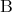 を
を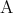 の必要条件という。命題
の必要条件という。命題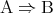 と命題
と命題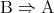 が共に真であるとき
が共に真であるとき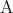 を
を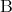 の必要十分条件といい
の必要十分条件といい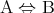 と書く。明らかに、このとき
と書く。明らかに、このとき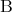 は
は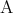 の必要十分条件でもある。
の必要十分条件でもある。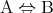 であるとき命題
であるとき命題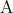 と
と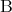 は同値であるともいう。同値な命題を同じ命題と考えることもある。
は同値であるともいう。同値な命題を同じ命題と考えることもある。
二つの命題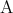 ,
, 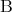 が同時に真であるときに真であると定めた命題を
が同時に真であるときに真であると定めた命題を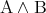 と書き
と書き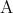 かつ
かつ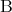 と読む。二つの命題
と読む。二つの命題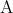 ,
, 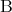 の少なくとも一方が真であるときに真であると定めた命題を
の少なくとも一方が真であるときに真であると定めた命題を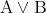 と書き
と書き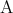 または
または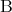 と読む。
と読む。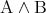 を
を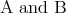 、
、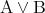 を
を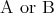 などとも書く。
などとも書く。
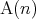
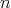 は
は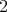 の倍数である。
の倍数である。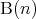
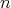 は
は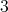 の倍数である。
の倍数である。とすれば
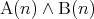
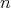 は
は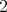 の倍数であり、かつ
の倍数であり、かつ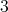 の倍数である。
の倍数である。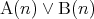
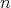 は
は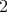 の倍数、または
の倍数、または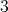 の倍数である。
の倍数である。などとなる。明らかに
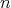 は
は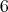 の倍数である。
の倍数である。
は 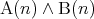 であるための必要十分条件である。
であるための必要十分条件である。
命題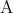 に対して、
に対して、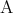 が偽のときに真と定めた命題を
が偽のときに真と定めた命題を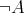 と書き
と書き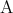 の否定、または
の否定、または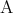 でないと読む。明らかに
でないと読む。明らかに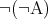 は
は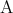 の必要十分条件である。
の必要十分条件である。
命題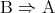 が真であるとき、命題
が真であるとき、命題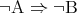 は常に真となる。これを
は常に真となる。これを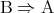 の対偶という。
の対偶という。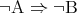 の対偶は
の対偶は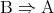 となるので、
となるので、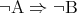 であることは
であることは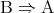 となることの必要十分条件である。
となることの必要十分条件である。
対偶が常に真であるということは次のように考えると理解しやすい。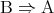 ということは、
ということは、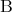 が
が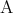 よりも “強い” ということである。図で表すと Figure
1.1
のようになる。
よりも “強い” ということである。図で表すと Figure
1.1
のようになる。
よってこのとき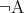 は
は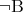 よりも “強く”、
よりも “強く”、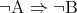 が成り立つのである。
が成り立つのである。
命題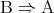 を考える。
を考える。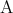 が真であれば、この命題は常に真である。例えば
が真であれば、この命題は常に真である。例えば
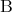 ならば
ならば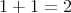 である。
である。
という命題は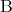 が真であるか偽であるかにかかわらず、常に真である。この対偶を考えると
が真であるか偽であるかにかかわらず、常に真である。この対偶を考えると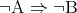 は
は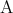 が真、すなわち
が真、すなわち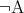 が偽であれば常に真となる。よって命題
が偽であれば常に真となる。よって命題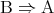 は
は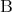 が偽であれば
が偽であれば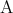 が真であるか偽であるかにかかわらず、常に真である。
が真であるか偽であるかにかかわらず、常に真である。
論理についての基本的な事柄をまとめておく。証明は与えない。同様のことが後に学ぶ集合に対しても成り立つ。
注意. 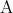 が偽であれば、任意の命題
が偽であれば、任意の命題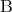 に対して
に対して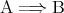 は真になるのだが、これが感覚的に受け入れがたいという学生も少なくはない。先の説明では
は真になるのだが、これが感覚的に受け入れがたいという学生も少なくはない。先の説明では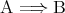 を感覚的に理解したが、正確には
を感覚的に理解したが、正確には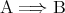 の定義が
の定義が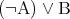 であり、認めてもらうしかない。
であり、認めてもらうしかない。
前の節で述べたことを理解するには真理表と呼ばれる表を用いるとよい。ある命題が真であることを , 偽であることを
, 偽であることを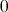 と表すことにする。二つの命題
と表すことにする。二つの命題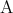 ,
, 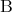 を考えるとき、それが真であるか偽であるかの可能性は 4 通りある。
を考えるとき、それが真であるか偽であるかの可能性は 4 通りある。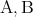 によって定まる基本的な命題については以下の通りである。
によって定まる基本的な命題については以下の通りである。
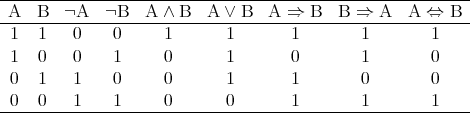
注意. 先に述べたように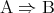 の定義は
の定義は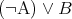 である。
である。
数学では「任意の に対して
に対して である」とか「ある
である」とか「ある が存在して
が存在して である」などという言い方がよく使われる。これらの意味をきちんと理解していないと、証明などが理解できない。まずは例を見てみよう。
である」などという言い方がよく使われる。これらの意味をきちんと理解していないと、証明などが理解できない。まずは例を見てみよう。
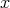 に対して
に対して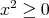 である。
である。
A の否定は何であろうか。 A が偽であるということは、一つでも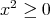 が成り立たない実数
が成り立たない実数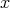 が存在すればよい。したがって
が存在すればよい。したがって
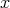 が存在して
が存在して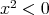 である。
である。
となる。より自然にいえば「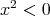 となる実数
となる実数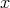 が存在する」ということになる。次に実数列
が存在する」ということになる。次に実数列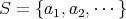 に対して次の命題を考える。
に対して次の命題を考える。
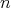 が存在して
が存在して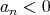 である。
である。
この否定は何であろうか。一つでも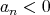 となる自然数
となる自然数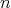 が存在すれば
が存在すれば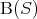 は真になるので、
は真になるので、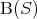 が偽になるためには、すべての自然数
が偽になるためには、すべての自然数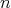 に対して
に対して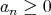 でなければならない。よって
でなければならない。よって
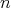 に対して
に対して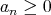 である。
である。となる。
以上のように「任意の に対して
に対して である」と「ある
である」と「ある が存在して
が存在して である」ということは、否定によって互いに移り会うものなのである。しっかりと覚えておこう。
である」ということは、否定によって互いに移り会うものなのである。しっかりと覚えておこう。
数学の教科書などでは、先の例のように命題をきちんと文章で表している場合がほとんどであるが、講義などでは適当に省略した記号を用いる場合が多い。この記号が理解できないことも講義が分からなくなる一つの要因である。ここできちんと理解しておこう。
まず、数学でよく用いられる記号を確認する。
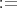 自然数全体の集合 (
自然数全体の集合 (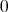 を含める場合もあるが、ここでは含めない)
を含める場合もあるが、ここでは含めない)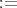 整数全体の集合 (普通の整数は有理整数ともいう)
整数全体の集合 (普通の整数は有理整数ともいう)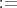 有理数全体の集合
有理数全体の集合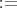 実数全体の集合
実数全体の集合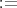 複素数全体の集合
複素数全体の集合
非負整数全体を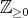 , 負の整数全体を
, 負の整数全体を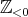 などと書くこともある。
などと書くこともある。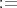 の記号は左辺を右辺で定めるという意味であるが、人によって違う記号を用いる場合もある。また集合という言葉は後できちんと説明するが、ここでは単に「自然数全体の集まり」のように理解すればよい。
の記号は左辺を右辺で定めるという意味であるが、人によって違う記号を用いる場合もある。また集合という言葉は後できちんと説明するが、ここでは単に「自然数全体の集まり」のように理解すればよい。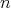 が自然数であるということを
が自然数であるということを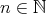 と表す。他の記号についても同様である。
と表す。他の記号についても同様である。
さて「任意の自然数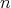 に対して
に対して 」ということを記号で「
」ということを記号で「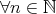 に対して
に対して 」などと書く。「ある自然数
」などと書く。「ある自然数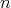 に対して
に対して 」ということは記号で「
」ということは記号で「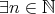 に対して
に対して 」などと書く。
」などと書く。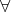 は All の A を引っくり返したもの、
は All の A を引っくり返したもの、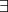 は Exists の E を引っくり返したものである。次の命題はすべて同じことを言っている。
は Exists の E を引っくり返したものである。次の命題はすべて同じことを言っている。
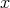 に対して
に対して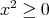 である。
である。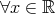 に対して
に対して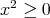 である。
である。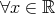 ,
, 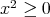 .
.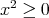 ,
, 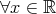 .
.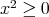 for all
for all 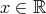 .
.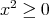 for any
for any 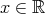 .
.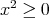 for every
for every 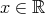 .
.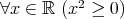 .
.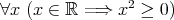 .
.all, any, every は英語としては、その与えるニュアンスが異なるが、論理的には同じと思ってよい。同様に次も同じことである。
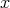 に対して
に対して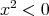 である。
である。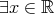 に対して
に対して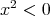 である。
である。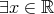 ,
, 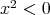 .
.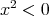 ,
, 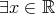 .
.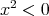 であるような
であるような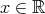 が存在する。
が存在する。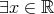 such that
such that 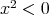 .
.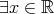 s.t.
s.t. 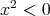 .
.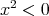 for some
for some 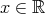 .
.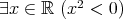 .
.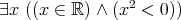 .
.
「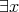 such that
such that 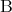 」というのは「
」というのは「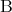 であるような
であるような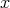 が存在する」ということを英語で言っているだけである。「such that」を省略して「s.t.」と書くことも多い。次の二つの命題を考えよう。
が存在する」ということを英語で言っているだけである。「such that」を省略して「s.t.」と書くことも多い。次の二つの命題を考えよう。
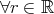 ,
, 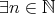 ,
, 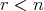 .
.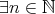 ,
, 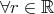 ,
, 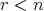 .
.この二つは記述してある順番が違うだけである。同じ意味だろうか。実はこれは全く違う意味なのである。それは文章にして読んでみれば分かる。
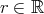 に対して、ある
に対して、ある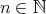 が存在して
が存在して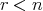 である。
である。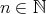 が存在して、任意の
が存在して、任意の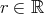 に対して
に対して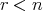 である。
である。
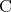 は与えられた
は与えられた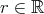 に対して
に対して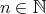 を決めればよいので真である。一方
を決めればよいので真である。一方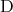 は
は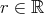 に関係なく
に関係なく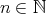 が存在しなければならず偽である。このように省略した記号は便利ではあるが、間違えをおかしやすいものである。試験の答案などにはきちんとした文章を書くことを勧める。
が存在しなければならず偽である。このように省略した記号は便利ではあるが、間違えをおかしやすいものである。試験の答案などにはきちんとした文章を書くことを勧める。
注意. 上の命題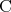 をより自然な言葉で「任意の
をより自然な言葉で「任意の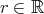 に対して
に対して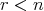 となるような
となるような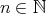 が存在する」と読むこともできる。しかしこの場合、
が存在する」と読むこともできる。しかしこの場合、
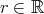 に対して、
に対して、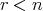 となるような
となるような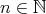 が存在する
が存在する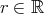 に対して
に対して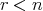 、となるような
、となるような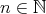 が存在する
が存在する
と句点を入れてみると (1) は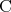 を、 (2) は
を、 (2) は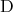 を表している。このように命題を記述する場合には、その意味が明らかとなるように細心の注意が必要となる。通常は、句点がない場合にもその文脈からどちらの意味であるかが読み取れることが多いが、少なくとも試験ではきちんと区別しなくてはならない。
を表している。このように命題を記述する場合には、その意味が明らかとなるように細心の注意が必要となる。通常は、句点がない場合にもその文脈からどちらの意味であるかが読み取れることが多いが、少なくとも試験ではきちんと区別しなくてはならない。
上の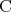 ,
, 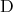 の否定を求めておく。文章から否定を考えるのはやや難しいが、記号を用いた場合には簡単であることが分かるだろう。
の否定を求めておく。文章から否定を考えるのはやや難しいが、記号を用いた場合には簡単であることが分かるだろう。
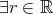 ,
, 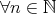 ,
, 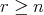 .
.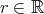 があって、任意の
があって、任意の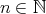 に対して
に対して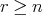 である。
である。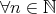 ,
, 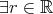 ,
, 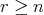 .
.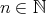 に対して、ある
に対して、ある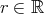 があって
があって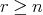 である。
である。
もちろん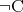 は偽で
は偽で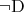 は真である。
は真である。
これをもう少し詳しく説明しよう。命題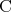 は丁寧に書くと以下のようになる。
は丁寧に書くと以下のようになる。
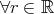 (
(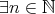 (
(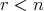 )).
)).
ここで (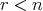 ) は
) は と
と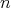 に関する命題である。 (
に関する命題である。 (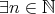 (
(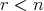 )) は
)) は のみに関する命題である。なぜならば
のみに関する命題である。なぜならば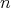 はこの中で定義されているので、これは特定の
はこの中で定義されているので、これは特定の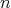 に関することをいっている訳ではないからである。同様に考えて命題
に関することをいっている訳ではないからである。同様に考えて命題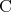 はどの変数にも依存しない命題である。
はどの変数にも依存しない命題である。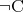 は以下のように解釈される。
は以下のように解釈される。
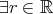
 (
(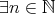 (
(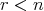 )).
)).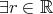 (
(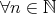
 (
(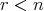 )).
)).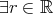 (
(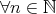 (
(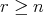 )).
)).
例1.3.1 ( -
-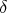 論法). 関数
論法). 関数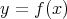 が
が で連続であるとは、以下の条件を満たすこととして定義される。
で連続であるとは、以下の条件を満たすこととして定義される。
[定義] 任意の正の数 に対して、ある正の数
に対して、ある正の数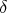 があって
があって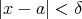 ならば
ならば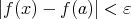 が成り立つ。
が成り立つ。
例えば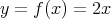 という関数は任意の
という関数は任意の において連続であるが、それは以下のように証明される。
において連続であるが、それは以下のように証明される。
証明.  を任意の正の数とする。
を任意の正の数とする。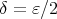 とする。このとき
とする。このとき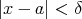 ならば
ならば
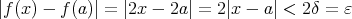
ここで重要なのは「ある正の数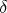 があって」といっているので本当に
があって」といっているので本当に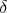 を決めてやる必要があるということである。
を決めてやる必要があるということである。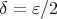 というのは本質的ではなく、例えば
というのは本質的ではなく、例えば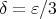 でも構わない。存在することをいいたいのだから、少なくとも一つの例を見せればいいのである。
でも構わない。存在することをいいたいのだから、少なくとも一つの例を見せればいいのである。
さて、次に連続でないことを証明してみよう。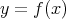 は
は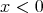 のとき
のとき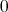 で
で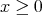 のとき
のとき で定めるとする。このとき、この関数は
で定めるとする。このとき、この関数は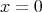 で連続でないことは分かるだろう。これを上の定義にしたがって証明する。連続でないことを示したいので定義を否定すればよい。このままで考えるとやや難しいので、連続の定義を記号を用いて書き直してみる。
で連続でないことは分かるだろう。これを上の定義にしたがって証明する。連続でないことを示したいので定義を否定すればよい。このままで考えるとやや難しいので、連続の定義を記号を用いて書き直してみる。
[定義] 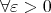 ,
, 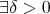 ,
, 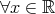 (
(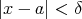
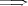
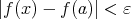 ).
).
これを否定するので、連続でないということは
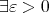 ,
, 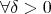
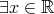
 (
(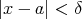
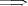
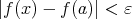 ).
).
 (
(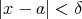
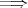
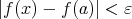 ) は「
) は「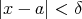 and
and 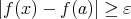 」ということである (問
1.2.4
)。したがって、いいたいことは
」ということである (問
1.2.4
)。したがって、いいたいことは
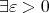 ,
, 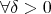 ,
, 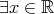 ((
((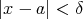 )
) 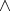 (
(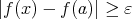 )).
)).
ということになる。さて証明をしてみよう。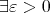 となっているので
となっているので をきちんと決めてやらなくてはならないことに注意する。
をきちんと決めてやらなくてはならないことに注意する。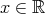 も同様に決めてやる必要がある。
も同様に決めてやる必要がある。
証明. 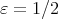 とする。任意の
とする。任意の 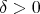 に対して
に対して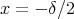 とすれば
とすれば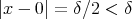 であって
であって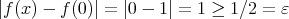 である。 (証明終り)
である。 (証明終り)
この証明で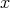 は
は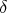 によって決まっていることに注意しよう。このような場合「
によって決まっていることに注意しよう。このような場合「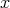 の取り方は
の取り方は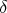 に依存する」などという言い方をする。またこの場合も
に依存する」などという言い方をする。またこの場合も や
や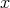 はこのように決めなくてはならないわけではなく、例えば
はこのように決めなくてはならないわけではなく、例えば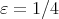 ,
, 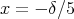 などでも構わない。
などでも構わない。 をどのように決めるかは問題によって異なり、自分で考えるしかない。
をどのように決めるかは問題によって異なり、自分で考えるしかない。
注意. 数学の講義では「命題 1.  」などと書かれることが多い。ここで言う命題とは「真である命題」を示している。その意味は「定理」、「補題」などと同じであると思ってよい。確認のため、よく使われる言葉などをまとめておこう。
」などと書かれることが多い。ここで言う命題とは「真である命題」を示している。その意味は「定理」、「補題」などと同じであると思ってよい。確認のため、よく使われる言葉などをまとめておこう。