環論演習15
理学部 数理・自然情報科学科 西田憲司演習問題
問 1.
整数を成分に持つ 2 次の正方行列の全体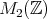 は行列の和と積に関して環である。
は行列の和と積に関して環である。
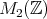 の部分集合
の部分集合
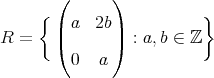
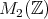 の部分環であることを示せ。また,
の部分環であることを示せ。また,
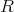 は整域かどうか調べよ。
は整域かどうか調べよ。
問 2.
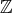 のイデアル (2),(6) および
のイデアル (2),(6) および
![ℚ [x]](img/el2949x.gif) のイデアル
のイデアル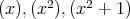 について答えよ。
について答えよ。
- (1)極大イデアルはどれか。
- (2)
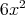 を含むイデアルはどれか。
を含むイデアルはどれか。
- (3)
剰余環
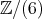 と
と
![2ℚ[x]∕(x )](img/el2953x.gif) は整域でないことを示せ。
は整域でないことを示せ。
問3.
整数環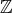 の積閉集合
の積閉集合
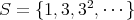 とする。
とする。
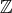 の素イデアル
の素イデアル
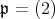 とする。
このとき,
とする。
このとき,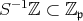 を示せ。
を示せ。
問 4.
![ℤ [x]](img/el2959x.gif) の元
の元
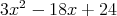 と
と
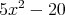 の最大公約数,最小公倍数を求めよ。
の最大公約数,最小公倍数を求めよ。
問 5.
素数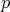 に対し,
に対し,
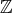 のイデアル
のイデアル
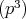 の根基
の根基
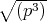 を求めよ。
を求めよ。
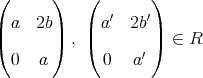 ならば,
ならば,
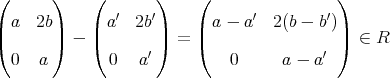
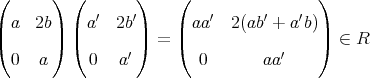
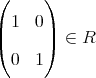
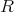 は
は
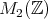 の部分環である。
の部分環である。

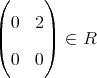 であるが,
であるが,
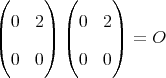
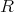 は整域ではない。
は整域ではない。
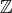 に対しては素数を,
に対しては素数を,
![ℚ [x]](img/el2977x.gif) に対しては既約な多項式を見つければよいのだか
ら,極大イデアルは
に対しては既約な多項式を見つければよいのだか
ら,極大イデアルは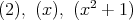 である。
である。
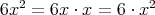 であるから,
であるから,
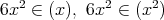 である。
である。
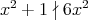 であるから,
であるから,
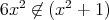 である。
である。
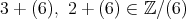 であり,
であり,
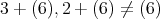 であるが,
であるが,
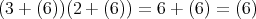 より,
より,
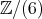 は整域ではない。
また,
は整域ではない。
また,
![x + (x2) ∈ ℚ [x]∕ (x2 )](img/el2987x.gif) で,
で,
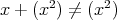 であるが,
であるが,
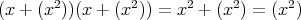 より,
より,
![2ℚ [x]∕(x )](img/el2990x.gif) は整域ではない。
は整域ではない。

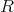 を環
を環
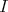 を
を
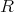 のイデアルとすると,
のイデアルとすると,
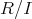 が整域
が整域
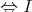 は素イデアル
は素イデアル
![ℤ, ℚ [x]](img/el2997x.gif) は単項イデアル整域であるから,素イデアル
は単項イデアル整域であるから,素イデアル
 極大イデアルなので(1) の結果から,
極大イデアルなので(1) の結果から,
![ℤ ∕(6), ℚ[x]∕(x2)](img/el2999x.gif) はいずれも整域ではない。
はいずれも整域ではない。
 は奇数全体の集合,すなわち
は奇数全体の集合,すなわち
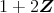 であるから,
であるから,
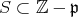 である。よって
である。よって
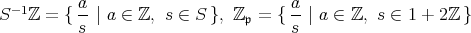 であるから,
であるから,
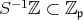 である。
である。

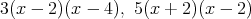 であるから,最大公約数は
であるから,最大公約数は
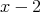 ,最小公倍数は
,最小公倍数は
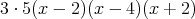 である。
である。
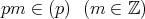 に対し,
に対し,
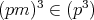 であるから,
であるから,
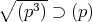 である。また,任意の
である。また,任意の
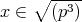 に対し,ある
に対し,ある
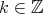 が存在して,
が存在して,
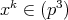 となるが,このとき
となるが,このとき
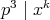 であり
であり
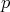 が素数であることから,
が素数であることから,
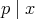 である。したがって,
である。したがって,
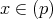 であり,
であり,
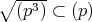 である。以上から,
である。以上から,