環論演習14
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
環準同型![φ : R [x] -→ C](img/el2889x.gif) を
を
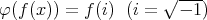 によって定める。次の問に答えよ。
によって定める。次の問に答えよ。
- (1)
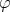 は全射であることを示せ。
は全射であることを示せ。
- (2)
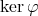 を求めよ。
を求めよ。
- (3)
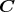 はある
はある
![R [x]](img/el2894x.gif) の剰余環と同型であることを示せ。
の剰余環と同型であることを示せ。
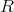 を可換環とし,
を可換環とし,
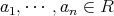 とする。このとき,
とする。このとき,
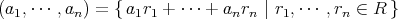
![φ : R [x] -→ C](img/el2889x.gif) を
を
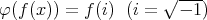 によって定める。次の問に答えよ。
によって定める。次の問に答えよ。
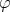 は全射であることを示せ。
は全射であることを示せ。
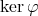 を求めよ。
を求めよ。
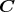 はある
はある
![R [x]](img/el2894x.gif) の剰余環と同型であることを示せ。
の剰余環と同型であることを示せ。
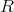 を可換環とし,
を可換環とし,
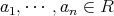 とする。このとき,
とする。このとき,
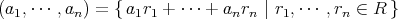
任意の
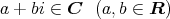 に 対 し,
に 対 し,
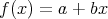 と お け ば,
と お け ば,
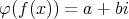 であるから
であるから
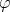 は全射である。
は全射である。

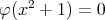 であるから,
であるから,
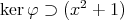 である。なぜなら,任意の
である。なぜなら,任意の
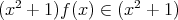 に対して,
に対して,
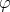 は環準同型であるから,
は環準同型であるから,
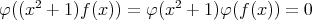 逆に,
逆に,
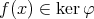 ならば,
ならば,
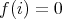 であるから,因数定理により
であるから,因数定理により
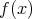 は
は
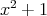 で割り切れる。したがって,
で割り切れる。したがって,
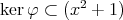 である。よって,
である。よって,
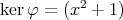
準同型定理より,
![R [x]∕ker φ ~= Im φ](img/el2914x.gif) であるが,
であるが,
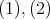 より,
より,
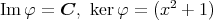 であるから,
であるから,
![R [x]∕(x2 + 1) ~ C =](img/el2917x.gif)

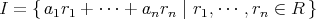 とおく。このとき任意の
とおく。このとき任意の
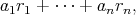
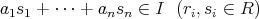 に対し,
に対し,
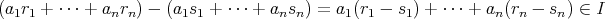
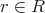 に対し,
に対し,
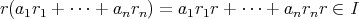 であるから,
であるから,
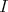 は
は
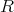 のイデアルである。また,任意の
のイデアルである。また,任意の
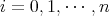 に対し,
に対し,
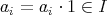 より,
より,
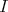 は
は
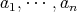 を含む
を含む
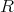 のイデアルである。したがって,
のイデアルである。したがって,
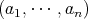 とは,
とは,
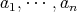 をすべて含むような
をすべて含むような
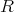 のイデアルで最小のものであったから,
のイデアルで最小のものであったから,
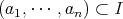 である。逆に,任意の
である。逆に,任意の
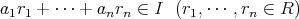 に対し,
に対し,
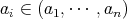 より,イデアルの定義から
より,イデアルの定義から
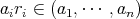 であり
であり
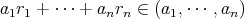 である。したがって,
である。したがって,
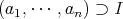 であり,
であり,
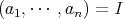 が示された。
が示された。
