環論演習13
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
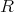 を環とし,
を環とし,
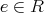 は
は
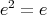 をみたすとする。
をみたすとする。
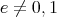 ならば,
ならば,
 は零因子であること
を示せ。
は零因子であること
を示せ。
問 2.
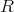 を可換環とし,
を可換環とし,
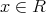 とする。このとき,
とする。このとき,
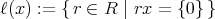
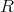 のイデアルであることを示せ。
のイデアルであることを示せ。
問 3.
- (1)
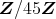 のイデアルをすべて求めよ。
のイデアルをすべて求めよ。
- (2)
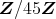 の素イデアルはどれか。
の素イデアルはどれか。
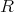 を環とし,
を環とし,
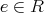 は
は
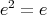 をみたすとする。
をみたすとする。
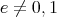 ならば,
ならば,
 は零因子であること
を示せ。
は零因子であること
を示せ。
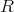 を可換環とし,
を可換環とし,
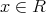 とする。このとき,
とする。このとき,
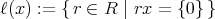
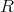 のイデアルであることを示せ。
のイデアルであることを示せ。
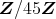 のイデアルをすべて求めよ。
のイデアルをすべて求めよ。
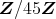 の素イデアルはどれか。
の素イデアルはどれか。
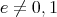 であるから,
であるから,
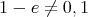 である。ところが,
である。ところが,
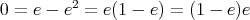 であるから,
であるから,
 は零因子である。
は零因子である。

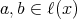 とする。このとき,
とする。このとき,
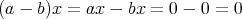 であるから,
であるから,
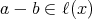 また,任意の
また,任意の
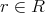 に対し,
に対し,
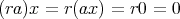 であるから,
であるから,
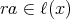 以上から,
以上から,
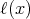 は
は
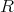 のイデアルである。
のイデアルである。

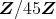 のイデアルは
のイデアルは
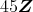 を含む
を含む
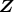 のイデアル
のイデアル
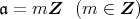 によって,
によって,
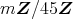 の形をしている (環論演習 5 の (2) 参照)。したがって,
の形をしている (環論演習 5 の (2) 参照)。したがって,
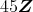 を含む
を含む
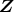 のイデアルをすべて求めれば良いが, p.92 の補題 2.4.1 より,
のイデアルをすべて求めれば良いが, p.92 の補題 2.4.1 より,
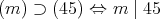 であるから, 45 の約数を調べればよい。したがって,
であるから, 45 の約数を調べればよい。したがって,
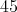 の約数は
の約数は
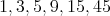 であるから,
であるから,
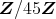 のすべてのイデアルは,
のすべてのイデアルは,
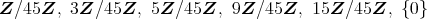 である。
である。
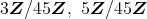 は素イデアルである。また,
は素イデアルである。また,
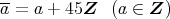 と表すことにすると,
と表すことにすると,
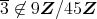 であるが,
であるが,
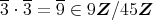 であるから,
であるから,
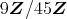 は素イデアルではない。さらに,
は素イデアルではない。さらに,
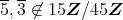 であるが,
であるが,
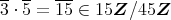 であるから,
であるから,
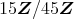 も素イデアルではない。同様に,
も素イデアルではない。同様に,
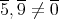 であるが,
であるが,
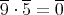 であるから,
であるから,
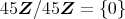 も素イデアルではない。以上から,素イデアルは
も素イデアルではない。以上から,素イデアルは
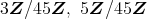 である。
である。
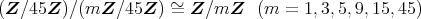 であるから,
であるから,
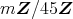 が素イデアルであることと
が素イデアルであることと
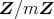 が整域であることと同値である。それはさらに,
が整域であることと同値である。それはさらに,
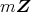 が素イデアルであることと同値なのだから,
が素イデアルであることと同値なのだから,
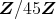 の素イデアルは
の素イデアルは
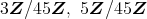 である。
である。