環論演習12
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
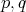 が相異なる素数のとき,
が相異なる素数のとき,
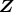 のイデアル
のイデアル
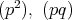 に対して
に対して
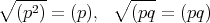
問2.
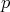 が素数のとき,
が素数のとき,
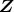 のイデアル
のイデアル
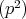 について次の問に答えよ。
について次の問に答えよ。
- (1)
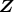 のイデアル
のイデアル
 が
が
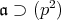 ならば
ならば
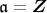 または
または
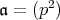 または
または
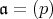 を
示せ。
を
示せ。
- (2)
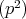 は既約なイデアル,を示せ。
は既約なイデアル,を示せ。
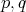 が相異なる素数のとき,
が相異なる素数のとき,
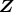 のイデアル
のイデアル
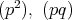 に対して
に対して
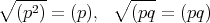
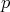 が素数のとき,
が素数のとき,
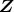 のイデアル
のイデアル
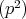 について次の問に答えよ。
について次の問に答えよ。
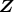 のイデアル
のイデアル
 が
が
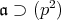 ならば
ならば
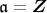 または
または
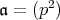 または
または
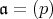 を
示せ。
を
示せ。
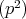 は既約なイデアル,を示せ。
は既約なイデアル,を示せ。
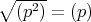 であること:
であること:
任意の
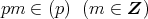 に対して,
に対して,
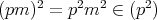 であるから,
であるから,
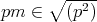 である。よって,
である。よって,
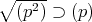 また,
また,
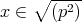 ならば,ある
ならば,ある
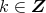 が存在し,
が存在し,
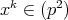 となるから,
となるから,
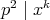 であり,
であり,
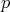 は素数であるから,
は素数であるから,
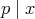 でなければならない。したがって,
でなければならない。したがって,
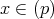 であるから,
であるから,
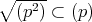 以上から,
以上から,
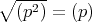 である。
である。
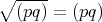 であること:
であること:
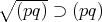 であることは明らかなので,
であることは明らかなので,
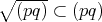 であることを示せばよい。
であることを示せばよい。
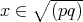 ならば,ある
ならば,ある
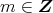 が存在し,
が存在し,
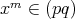 となるから,このとき
となるから,このとき
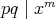 である。今,
である。今,
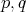 は相異なる素数であるから,
は相異なる素数であるから,
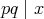 でなければならない。したがって,
でなければならない。したがって,
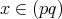 であり,
であり,
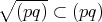

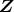 は単項イデアル整域であるから,
は単項イデアル整域であるから,
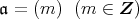 と表しておく。 p.92 の補題 2.4.1 より,
と表しておく。 p.92 の補題 2.4.1 より,
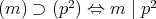 であるから,
であるから,
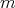 は
は
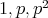 のいずれかである。したがって,
のいずれかである。したがって,
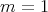 の と き,
の と き,
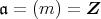 ,
,
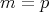 の と き,
の と き,
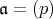 ,
,
 のとき,
のとき,
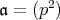 である。
である。

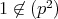 であるから,
であるから,
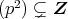 であることはよい。また,
であることはよい。また,
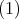 の結果から
の結果から
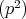 を真に含む
を真に含む
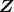 のイデアルは
のイデアルは
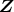 と
と
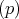 しかなく,
しかなく,
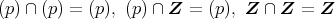 であるから,
であるから,
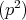 は既約なイデアルである。
は既約なイデアルである。
