環論演習11
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
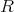 は可換環,
は可換環,
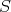 を
を
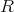 の積閉集合とする。
の積閉集合とする。
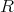 の
の
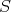 による商環
による商環
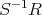 のイデアルは全て次の
のイデアルは全て次の
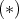 の様に表されることは証明されている:
の様に表されることは証明されている:

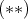 を示せ。
を示せ。
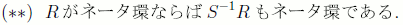
問2.
![Z [x]](img/el2715x.gif) の部分環
の部分環
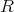 を
を
![R = Z [2x,2x2, 2x3,⋅⋅⋅]](img/el2717x.gif)
![n f(x) = anx + ⋅⋅⋅ + a1x + a0 ∈ Z [x]](img/el2718x.gif) について,
について,
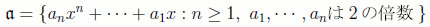
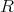 の部分集合
の部分集合
 を
を
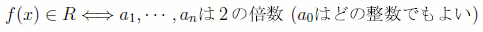
- (1)
 は
は
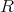 のイデアルを示せ。
のイデアルを示せ。
- (2)
 は有限生成でないことを示せ(従って
は有限生成でないことを示せ(従って
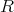 はネータ環ではない。)
はネータ環ではない。)
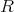 は可換環,
は可換環,
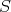 を
を
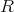 の積閉集合とする。
の積閉集合とする。
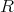 の
の
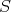 による商環
による商環
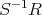 のイデアルは全て次の
のイデアルは全て次の
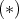 の様に表されることは証明されている:
の様に表されることは証明されている:

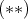 を示せ。
を示せ。
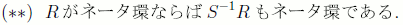
![Z [x]](img/el2715x.gif) の部分環
の部分環
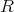 を
を
![R = Z [2x,2x2, 2x3,⋅⋅⋅]](img/el2717x.gif)
![n f(x) = anx + ⋅⋅⋅ + a1x + a0 ∈ Z [x]](img/el2718x.gif) について,
について,
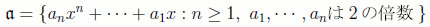
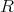 の部分集合
の部分集合
 を
を
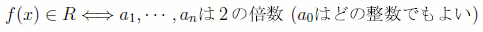
 は
は
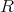 のイデアルを示せ。
のイデアルを示せ。
 は有限生成でないことを示せ(従って
は有限生成でないことを示せ(従って
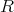 はネータ環ではない。)
はネータ環ではない。)
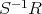 の任意のイデアルの無限上昇列を
の任意のイデアルの無限上昇列を
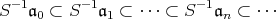
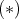 からこのような形をしている)このとき,各
からこのような形をしている)このとき,各
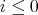 に対し,
に対し,
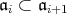 である。なぜなら,
である。なぜなら,
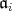 の任意の元
の任意の元
 に対し,
に対し,
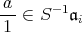 であるから,
であるから,
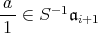 でもあり,
でもあり,
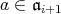 である。したがって,
である。したがって,
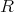 のイデアルの無限上昇列
のイデアルの無限上昇列
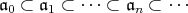
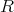 がネータ環であることから,ある
がネータ環であることから,ある
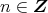 が存在して,
が存在して,
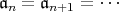 となる。したがって,このとき
となる。したがって,このとき
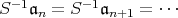 であるから,
であるから,
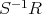 はネータ環である。
はネータ環である。

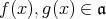 ならば,
ならば,
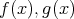 の定数項は
の定数項は
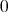 であるから
であるから
 の定数項も
の定数項も
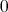 である。したがって,
である。したがって,
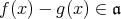 である。また,任意の
である。また,任意の
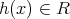 に対して,
に対して,
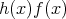 の定数項も
の定数項も
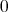 であるから,
であるから,
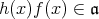 。よって,
。よって,
 は
は
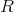 のイデアル。
のイデアル。

 が有限生成であると仮定し,
が有限生成であると仮定し,
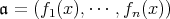 とおく。このとき,各生成元の次数の中で最大のものを
とおく。このとき,各生成元の次数の中で最大のものを
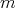 とおくと,任意の
とおくと,任意の
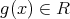 に対して
に対して
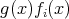 の
の
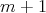 次の係数は
次の係数は
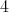 の倍数である。したがって
の倍数である。したがって
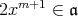 であるが,
であるが,
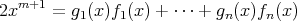
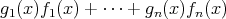 の
の
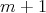 次の係数は 4 の倍数であるから
次の係数は 4 の倍数であるから
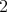 に
はなり得ないので矛盾。よって
に
はなり得ないので矛盾。よって
 は有限生成ではない。
は有限生成ではない。
