環論演習9
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
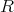 は domain (整域)とする。
は domain (整域)とする。
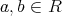 に対し,
に対し,
「
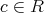 が
が
 と
と
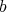 の最小公倍数となる必要十分条件は
の最小公倍数となる必要十分条件は
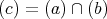 」
」
を示せ。
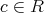 が
が
 と
と
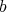 の最小公倍数となる必要十分条件は
の最小公倍数となる必要十分条件は
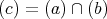 」
」
問2.
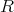 は問 1. と同じとする。
は問 1. と同じとする。
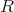 の元
の元
 と
と
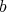 の最小公倍数を
の最小公倍数を
 とする。問 1. より
とする。問 1. より
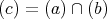 であるから,
であるから,
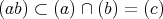 である。従って,
である。従って,
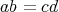 となる
となる
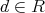 がある。このとき,
がある。このとき,
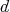 は
は
 と
と
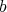 の最大公約数であることを示せ。
の最大公約数であることを示せ。
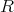 は domain (整域)とする。
は domain (整域)とする。
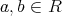 に対し,
に対し,
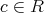 が
が
 と
と
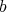 の最小公倍数となる必要十分条件は
の最小公倍数となる必要十分条件は
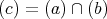 」
」
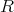 は問 1. と同じとする。
は問 1. と同じとする。
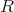 の元
の元
 と
と
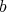 の最小公倍数を
の最小公倍数を
 とする。問 1. より
とする。問 1. より
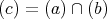 であるから,
であるから,
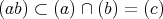 である。従って,
である。従って,
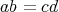 となる
となる
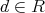 がある。このとき,
がある。このとき,
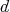 は
は
 と
と
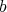 の最大公約数であることを示せ。
の最大公約数であることを示せ。
 が
が
 と
と
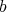 の最小公倍数であるとする。このとき,
の最小公倍数であるとする。このとき,
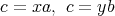 となるような
となるような
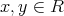 が存在する。したがって,任意の
が存在する。したがって,任意の
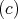 の元
の元
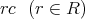 に対して
に対して
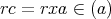 かつ
かつ
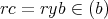 であるから,
であるから,
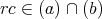 。よって,
。よって,
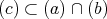 である。また,任意に
である。また,任意に
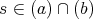 をとれば,
をとれば,
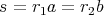 となるような,
となるような,
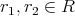 が存在するから,
が存在するから,
 は
は
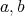 の公倍数である。よって,
の公倍数である。よって,
 は
は
 で割り切れるので,
で割り切れるので,
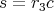 となる
となる
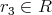 が存在するから,
が存在するから,
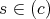 である。よって
である。よって
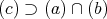 であり,
であり,
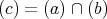 である。逆に,
である。逆に,
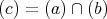 であるとする。このとき,
であるとする。このとき,
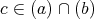 であるから,
であるから,
 は
は
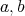 の公倍数である。したがって,
の公倍数である。したがって,
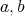 の公倍数が
の公倍数が
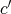 がすべて
がすべて
 で割り切れることを示せばよい。
で割り切れることを示せばよい。
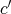 は
は
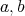 の公倍数であるから,
の公倍数であるから,
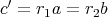 となるような,
となるような,
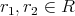 が存在するので,
が存在するので,
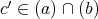 である。今,
である。今,
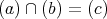 であるから,
であるから,
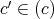 なので,
なので,
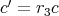 となるような
となるような
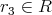 が存在するから,
が存在するから,
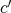 は
は
 で割り切れる。したがって,
で割り切れる。したがって,
 は
は
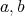 の最小公倍数である。
の最小公倍数である。

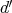 が
が
 と
と
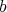 の公約数ならば,
の公約数ならば,
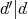 であることを示せばよい。
であることを示せばよい。
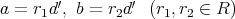 とおく。このとき,
とおく。このとき,
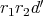 は
は
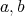 の公倍数であるから,
の公倍数であるから,
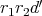 は最小公倍数
は最小公倍数
 で割り切れる。そこで,
で割り切れる。そこで,
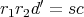 とおけば,
とおけば,
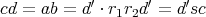 となる。
となる。
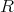 は整域であるから,
は整域であるから,
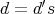 となり,
となり,
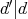 である。
である。
