環論演習8
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
- (1)
 は体
は体
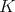 の付値とするとき,
の付値とするとき,
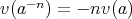 を示せ。 ただし,
を示せ。 ただし,
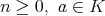 。
。
- (2)
有理数体
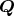 の
の
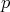 進付値
進付値
 は付値の条件 (2), (3) を充たすことを示せ。
付値の条件 (2)
は付値の条件 (2), (3) を充たすことを示せ。
付値の条件 (2)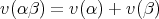
付値の条件 (3)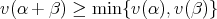
問2.
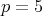 のとき,即ち 5 進付値を考える。このとき付値環は
のとき,即ち 5 進付値を考える。このとき付値環は

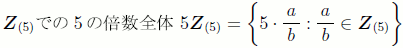
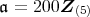 を含む
を含む
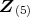 のイデアルをすべて
求めよ。
のイデアルをすべて
求めよ。
 は体
は体
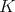 の付値とするとき,
の付値とするとき,
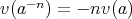 を示せ。 ただし,
を示せ。 ただし,
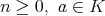 。
。
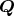 の
の
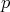 進付値
進付値
 は付値の条件 (2), (3) を充たすことを示せ。
は付値の条件 (2), (3) を充たすことを示せ。
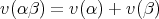
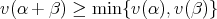
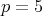 のとき,即ち 5 進付値を考える。このとき付値環は
のとき,即ち 5 進付値を考える。このとき付値環は

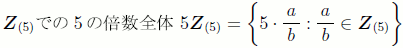
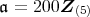 を含む
を含む
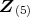 のイデアルをすべて
求めよ。
のイデアルをすべて
求めよ。
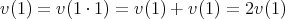 であるから,
であるから,
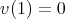 である。したがって,
である。したがって,
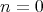 のときは正しい。
のときは正しい。
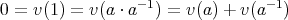 であるから,
であるから,
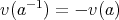 である。したがって,
である。したがって,
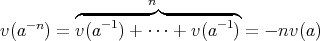 である。
である。

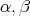 のどちらかが
のどちらかが
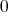 ならば,主張は明らかであるから,
ならば,主張は明らかであるから,
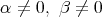 とする。
とする。
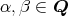 とし,
とし,
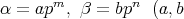 は分母,分子がいずれも
は分母,分子がいずれも
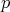 で割り切れないような分数,
で割り切れないような分数,
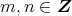 ) と表しておくと,
) と表しておくと,
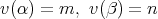 である。このとき,
である。このとき,
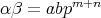 であり,
であり,
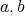 のとり方から,
のとり方から,
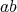 は分母,分子がいずれも
は分母,分子がいずれも
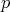 で割り切れないような分数である。したがって,
で割り切れないような分数である。したがって,
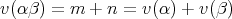 である。次に (3) についてだが,
である。次に (3) についてだが,
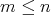 としてかまわない。このとき,
としてかまわない。このとき,
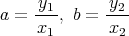 と表せば,
と表せば,
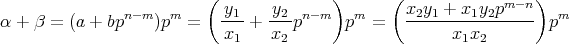
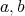 のとり方から,
のとり方から,
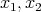 はいずれも
はいずれも
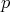 で割り切れない。よって,
で割り切れない。よって,
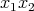 は
は
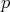 で割り切れず,さらに
で割り切れず,さらに
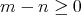 であることから,
であることから,
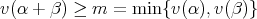

 の任意の元
の任意の元
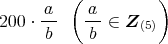 に対して,
に対して,
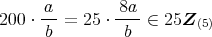 であり,
であり,
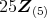 の任意の元
の任意の元
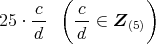 に対し,
に対し,
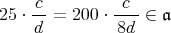 であるから,
であるから,
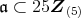 かつ
かつ
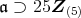 。よって,
。よって,
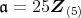 である。定理 2.3.5(3) から,
である。定理 2.3.5(3) から,
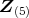 の真のイデアルはすべて付値イデアルのベキであり,
の真のイデアルはすべて付値イデアルのベキであり,
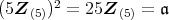 である。よって,
である。よって,
 を含むような
を含むような
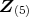 のイデアルは,
のイデアルは,
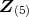 自身,
自身,
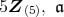 の 3 つである。
の 3 つである。