環論演習7
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
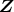 のイデアル
のイデアル
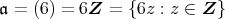 とする。
とする。
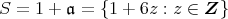 とおく。
とおく。
- (1)
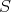 は積閉集合を示せ。
は積閉集合を示せ。
- (2)
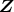 の
の
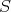 による商環
による商環
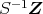 の中に,
の中に,
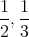 はあるか(即ち,
はあるか(即ち,
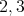 の逆元はあるか)?また,
の逆元はあるか)?また,
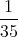 はあるか?
はあるか?
問 2.
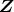 の積閉集合
の積閉集合
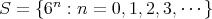 による商環
による商環
 を考える。
を考える。
- (1)
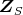 に
に
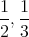 はあるか?また,
はあるか?また,
 はあるか?
はあるか?
- (2)
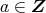 に対し,
に対し,
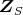 のイデアル
とする。このとき,
のイデアル
とする。このとき,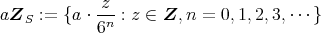
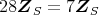 を示せ。また,
を示せ。また,
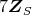 は
は
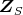 の素イデアルを示せ。
の素イデアルを示せ。
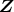 のイデアル
のイデアル
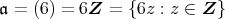 とする。
とする。
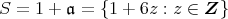 とおく。
とおく。
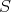 は積閉集合を示せ。
は積閉集合を示せ。
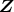 の
の
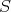 による商環
による商環
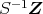 の中に,
の中に,
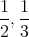 はあるか(即ち,
はあるか(即ち,
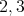 の逆元はあるか)?また,
の逆元はあるか)?また,
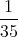 はあるか?
はあるか?
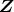 の積閉集合
の積閉集合
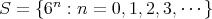 による商環
による商環
 を考える。
を考える。
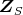 に
に
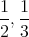 はあるか?また,
はあるか?また,
 はあるか?
はあるか?
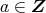 に対し,
に対し,
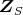 のイデアル
のイデアル
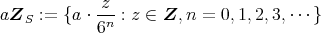
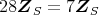 を示せ。また,
を示せ。また,
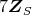 は
は
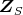 の素イデアルを示せ。
の素イデアルを示せ。
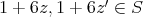 とすると,
とすると,
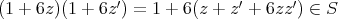 であり,
であり,
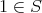 である。
である。

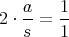 をみたすような
をみたすような
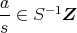 が存在したとすれば,ある
が存在したとすれば,ある
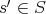 があって,
があって,
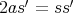 となってなくてはいけないが,左辺は偶数,右辺は
となってなくてはいけないが,左辺は偶数,右辺は
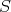 の元で奇数であるから矛盾する。したがって,
の元で奇数であるから矛盾する。したがって,
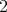 は単数ではない。同様に
は単数ではない。同様に
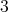 についても単数でないことがわかる。また,
についても単数でないことがわかる。また,
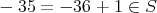 であるから,
であるから,
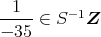 である。したがって,
である。したがって,
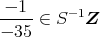 であり,
であり,
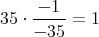 であるから,
であるから,
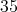 は単数である。
は単数である。
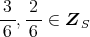 であり,
であり,
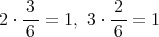 であるから,
であるから,
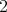 も
も
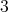 も単数である。また,
も単数である。また,
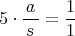 となるような
となるような
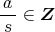 が存在したとすると,
が存在したとすると,
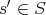 があって
があって
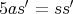 となっていなくてはいけない。ところが,右辺は
となっていなくてはいけない。ところが,右辺は
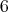 のベキであるから,
のベキであるから,
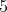 を素因数として含まないので矛盾する。したがって,
を素因数として含まないので矛盾する。したがって,
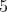 に逆元はない。
に逆元はない。
任意の
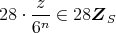 に対して,
に対して,
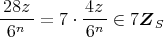 であるから,
であるから,
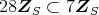 である。また,任意の
である。また,任意の
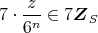 に対して,
に対して,
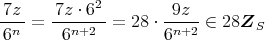 であるから,
であるから,
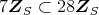 である。以上から,
である。以上から,
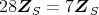 また,
また,
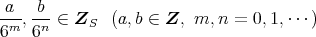 とし,
とし,
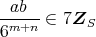 とする。このとき,
とする。このとき,
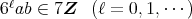 であるから, 7 は素数より
であるから, 7 は素数より
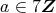 または
または
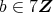 である。したがって,
である。したがって,
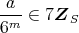 または,
または,
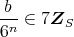 である。また,
である。また,
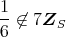 であることは容易にわかるから,
であることは容易にわかるから,
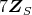 は
は
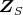 の真のイデアルである。以上から
の真のイデアルである。以上から
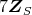 は素イデアルである。
は素イデアルである。
