環論演習6
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
定理 2.2.7 (極大イデアルの存在)の証明を真似て次を示せ。可換環
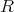 の積閉集合を
の積閉集合を
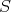 とする。このとき,
とする。このとき,
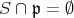 (空集合)となる素イデアル
(空集合)となる素イデアル
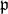 が存在する。
が存在する。Hint;
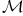 の替わりに
の替わりに
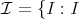 は
は
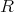 のイデアルで
のイデアルで
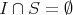 を充たす
を充たす
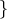 を考えよ。
を考えよ。
-
イデアル
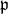 が素イデアル,を証明するために,
が素イデアル,を証明するために,
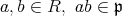 とし,更に,
とし,更に,
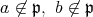 だったとして矛盾を出せ。
だったとして矛盾を出せ。
問2.
- (1)
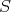 を
を
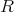 の積閉集合とする.
の積閉集合とする.
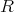 のイデアル
のイデアル
 に対し,
とおくとき,
に対し,
とおくとき,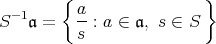
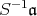 は
は
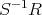 のイデアルであることを示せ。次に,
を示せ。
のイデアルであることを示せ。次に,
を示せ。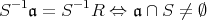
- 多項式環
![R = Q [x,y ]](img/el2379x.gif) の積閉集合
の積閉集合
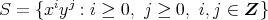 とするとき,
とするとき,
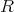 のイデアル
のイデアル
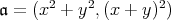 に対し,
に対し,
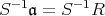 を示せ。
を示せ。
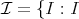 は
は
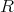 のイデアルで
のイデアルで
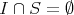 を充たす
を充たす
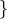 とおくと,
とおくと,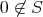 より,
より,
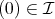 。
したがって
。
したがって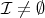 である。そこで,
である。そこで,
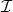 の任意の全順序部分集合
の任意の全順序部分集合
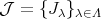 に対し,
に対し,
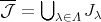 とすると,
とすると,
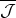 は
は
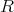 のイデアルである。なぜなら,
のイデアルである。なぜなら,
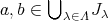 とすると,
とすると,
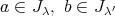 となるような,
となるような,
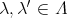 が存在するが,
が存在するが,
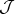 が全順序集合であるか
ら,
が全順序集合であるか
ら,
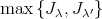 を考えることができ(すなわち
を考えることができ(すなわち
 ),今これ
を
),今これ
を
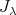 としておくと,
としておくと,
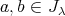 である。ここで,
である。ここで,
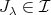 であるから
であるから
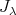 は
は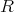 のイデアル
なので
のイデアル
なので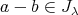 である。よって
である。よって
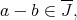 任意の
任意の
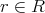 に対して
に対して
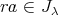 であるから,
であるから,
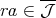 でもあり
でもあり
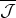 は
は
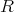 のイデアルであることが示された。また,任意の
のイデアルであることが示された。また,任意の
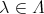 に対し
に対し
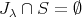 であるから,
であるから,
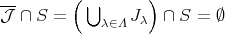 でもあるから,
でもあるから,
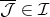 である。
である。
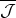 が
が
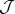 の上界であることは明らか。以上から,
の上界であることは明らか。以上から,
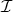 の任意の全順序部分集合が,
の任意の全順序部分集合が,
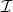 の
中に上界をもつことが示されたので,
の
中に上界をもつことが示されたので,
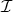 は帰納的順序集合である。よって,ツォルンの補題により
は帰納的順序集合である。よって,ツォルンの補題により
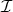 には極大元
には極大元
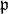 が存在する。この
が存在する。この
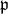 が素イデアルであることを示すために
が素イデアルであることを示すために
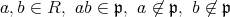 とする。このとき,
とする。このとき,
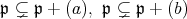 であるから,
であるから,
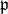 の極大性により,
の極大性により,
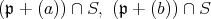 はいずれも空でない。したがって,
はいずれも空でない。したがって,
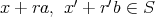 となるような,
となるような,
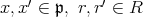 が存在し,
が存在し,
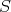 が積閉集合より,
が積閉集合より,
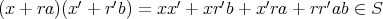 であるが,
であるが,
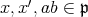 であるから,
であるから,
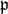 の元でもある。これは,
の元でもある。これは,
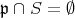 であることに矛盾する。
であることに矛盾する。

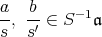 と す る と,
と す る と,
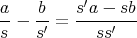 で あ り,
で あ り,
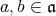 よ り,
よ り,
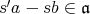
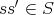 である。よって,
である。よって,
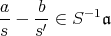 。また,
。また,
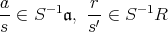 ならば,
ならば,
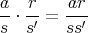 であり,
であり,
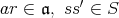 であるから
であるから
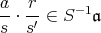 である。以上から
である。以上から
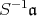 は
は
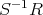 のイデアルである。次に,
のイデアルである。次に,
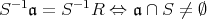
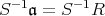 とすると,
とすると,
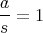 となるような,
となるような,
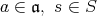 が存在する。このとき,
が存在する。このとき,
 となるような
となるような
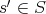 が存在するが,
が存在するが,
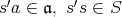 より,
より,
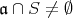 である。逆に,
である。逆に,
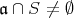 とすると,
とすると,
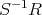 のイデアル
のイデアル
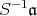 に単数が存在することになる。
したがって,
に単数が存在することになる。
したがって,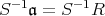 である。
である。

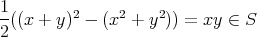 であるが,
であるが,
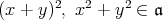 より,
より,
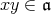 でもある。したがって,
でもある。したがって,
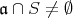 であるから, (1) の結果より,
であるから, (1) の結果より,