環論演習5
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
複素数体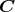 上の 1 変数多項式環
上の 1 変数多項式環
![R = C [x]](img/el2288x.gif) を考える。任意の複素数
を考える。任意の複素数
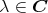 に対し
に対し
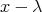 で生成された
で生成された
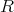 のイデアル
のイデアル
![𝔞λ = (x - λ) = {(x - λ)f (x) : f(x) ∈ C [x ]}](img/el2292x.gif)
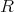 の極大イデアル,を示せ。
の極大イデアル,を示せ。
問2.
可換環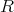 とそのイデアル
とそのイデアル
 が与えられている。このとき剰余環
が与えられている。このとき剰余環
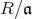 のイデアルは
のイデアルは
 を含む
を含む
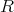 のイデアル
のイデアル
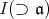 により,
により,
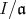 の形をしている。
の形をしている。
(ただし,
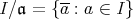 )
)
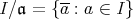 )
)
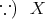 を
を
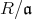 のイデアルとする。
のイデアルとする。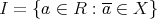 とおくと,
とおくと,
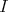 はイデアルの条件を充たすことが確かめられて,
はイデアルの条件を充たすことが確かめられて,
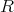 のイデアルになる。そして,任意の
のイデアルになる。そして,任意の
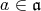 に対し,
に対し,
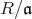 では
では
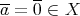 から
から
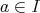 。よって,
。よって,
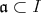 である。従って,
である。従って,
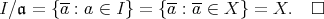
-
(1)体
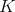 上の多項式環
上の多項式環
![K [x ]](img/el2314x.gif) のイデアル
のイデアル
![𝔞 = (f (x )), f (x ) ∈ K [x]](img/el2315x.gif) に対し,剰余環
に対し,剰余環
![K [x]∕ 𝔞](img/el2316x.gif) のイデアルは
のイデアルは
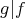 となる多項式
となる多項式
![g(x) ∈ K [x]](img/el2318x.gif) により,
により,
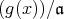 の形を
していることを示せ。 (上の事実を使う)
の形を
していることを示せ。 (上の事実を使う)
- (2)
![R = Q [x]∕(x2 - x - 6)](img/el2320x.gif) のイデアルをすべて求めよ。
のイデアルをすべて求めよ。
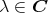 を任意に一つとって固定する。このとき,
を任意に一つとって固定する。このとき,
![Φλ : C [x] - → C](img/el2322x.gif) を
を
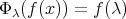 (多項式に
(多項式に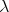 を代入する写像) によって定めると,
を代入する写像) によって定めると,
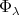 は環準同型となる。また,
は環準同型となる。また,
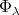 は全射である。なぜなら任意の
は全射である。なぜなら任意の
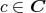 に対して,
に対して,
![f(x) ∈ C [x]](img/el2328x.gif) を定数多項式
を定数多項式
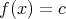 で定めれば
で定めれば
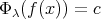 である。したがって,準同型定理により
である。したがって,準同型定理により
![C [x]∕Ker Φ ~= Cλ](img/el2331x.gif) であるから,
であるから,
![C [x]∕Ker Φ λ](img/el2332x.gif) は体であるが,
は体であるが,
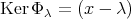 であることを示せば主張は証明される。実際,
であることを示せば主張は証明される。実際,
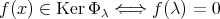

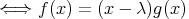 となるような
となるような
![g(x) ∈ C [x]](img/el2335x-2.gif) が存在する 。
が存在する 。
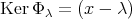 である。
である。

![K [x ]∕𝔞](img/el2338x.gif) のイデアルは
のイデアルは
 を含む
を含む
![K [x]](img/el2340x.gif) のイデアル
のイデアル
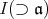 により,
により,
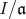 の形をしている。また,
の形をしている。また,
![K [x]](img/el2343x.gif) は単項イデアル整域(教科書 p.81 定理 2.2.4)
であるから,この
は単項イデアル整域(教科書 p.81 定理 2.2.4)
であるから,この
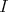 はある
はある
![g(x) ∈ K [x ]](img/el2345x.gif) により,
により,
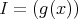 の形をしている。
ま た,
の形をしている。
ま た,
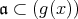 であるから,
であるから,
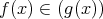 である。したがって,
である。したがって,
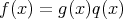 となるような
となるような
![q(x ) ∈ K [x]](img/el2350x.gif) が存在するから,
が存在するから,
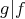 である。
である。

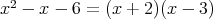 を割り切る多項式は,
を割り切る多項式は,
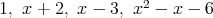 の4つである。 (1) の結果から,
の4つである。 (1) の結果から,
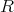 のイデアルは,
のイデアルは,
![(1)∕(x2 - x - 6) = Q [x ]∕(x2 - x - 6) = R, (x + 2 )∕ (x2 - x - 6 )](img/el2356x.gif)
