環論演習4
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
- (1)
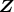 のイデアル
のイデアル
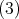 による剰余環
による剰余環
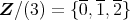 において次の問に答えよ。
において次の問に答えよ。
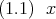 の方程式
の方程式
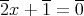 を解け。
を解け。
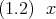 の方程式
の方程式
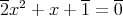 は
は
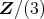 に解を持つか調べよ。
に解を持つか調べよ。
- (2)
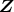 のイデアル
のイデアル
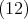 による剰余環
による剰余環
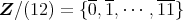 において次の問に答えよ。
において次の問に答えよ。
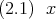 の方程式
の方程式
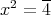 を解け。
を解け。
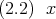 の方程式
の方程式
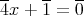 は
は
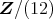 に解を持つか調べよ。
に解を持つか調べよ。
問2.
-
(1)複素数体の部分環
![Z [i] = {a + bi : a,b ∈ Z }](img/el2235x.gif) のイデアル
のイデアル
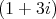 による剰余環
による剰余環
![R = Z [i]∕(1 + 3i)](img/el2237x.gif) を考える。
を考える。
![α ∈ Z [i]](img/el2238x.gif) を含む
を含む
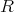 の剰余類を
の剰余類を
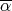 と記す。
と記す。
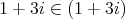 より,
より,
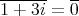 。 従って,
。 従って,
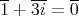 。
。
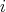 をかけて,
をかけて,
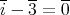 ,即ち,
,即ち,
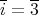 である。このことから,
である。このことから,
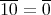 を示せ。
を示せ。
-
(2)環の準同型
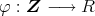 を
を
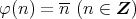 と定める。このとき,
と定める。このとき,
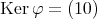 を示せ。 (実は
を示せ。 (実は
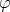 は全射なので,準同型定理より
は全射なので,準同型定理より
![Z ∕(10) ~= Z [i]∕)(1 + 3i)](img/el2252x.gif) である。)
である。)
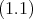 次のような表をかけばよい。
次のような表をかけばよい。
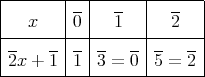

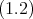 上と同様に次のような表をかけばよい。
上と同様に次のような表をかけばよい。
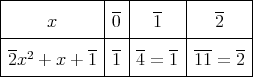
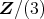 の中に解を持たない。
の中に解を持たない。
 これも(1) と同様すべて元を代入して表を作ればよい。
これも(1) と同様すべて元を代入して表を作ればよい。
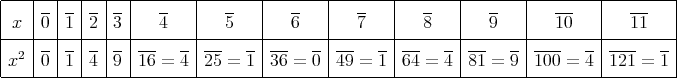 したがって,この方程式の解は
したがって,この方程式の解は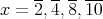 である。
である。
 これも表を作れば下のようになる。
これも表を作れば下のようになる。
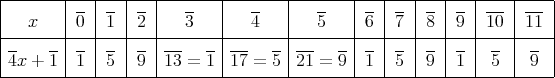 以上から,この方程式は
以上から,この方程式は
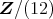 の中に解を持たない。
の中に解を持たない。
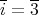 より,
より,
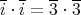 である。よって,
である。よって,
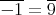 であるから,
であるから,
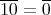

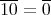 であるから,
であるから,
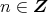 に対し,
に対し,
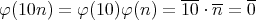 なので,
なので,
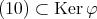 であることはよいから,
であることはよいから,
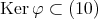 を示せばよい。
を示せばよい。
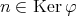 ,すなわち
,すなわち
 であるとすると,ある
であるとすると,ある
![Z [i]](img/el2277x.gif) の元
の元
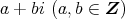 が存在して,
が存在して,
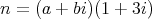 となる。このとき,
となる。このとき,
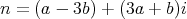 であるから,虚部を比較して
であるから,虚部を比較して
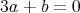 。よって
。よって
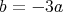 であり,これより実部を比較すれば
であり,これより実部を比較すれば
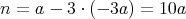 したがって,
したがって,
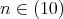 である。ゆえに
である。ゆえに