環論演習3
理学部 数理・自然情報科学科 西田憲司演習問題
問 1.
- (1)体
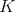 のイデアルはゼロイデアル
のイデアルはゼロイデアル
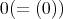 と
と
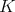 自身
自身
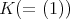 の2つのみであることを示せ。
逆に,可換環
の2つのみであることを示せ。
逆に,可換環
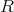 がゼロイデアルと
がゼロイデアルと
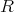 自身の 2 つしかイデアルを持たないならば
自身の 2 つしかイデアルを持たないならば
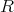 は体であることを示せ。
は体であることを示せ。
- (2)環
![Z[x]](img/el2111x.gif) の中で,
の中で,
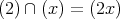 であることを示せ。
であることを示せ。
問 2.
- (1)
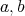 は整数とするとき,
は整数とするとき,
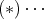
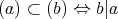 を証明せよ。
を証明せよ。
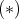 を用いて次を示せ:
を用いて次を示せ:

- (2)
計算により
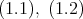 の逆の包含関係
の逆の包含関係
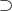 を示し,
を示し,

を証明せよ。
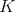 のイデアルはゼロイデアル
のイデアルはゼロイデアル
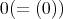 と
と
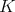 自身
自身
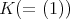 の2つのみであることを示せ。
逆に,可換環
の2つのみであることを示せ。
逆に,可換環
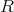 がゼロイデアルと
がゼロイデアルと
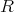 自身の 2 つしかイデアルを持たないならば
自身の 2 つしかイデアルを持たないならば
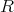 は体であることを示せ。
は体であることを示せ。
![Z[x]](img/el2111x.gif) の中で,
の中で,
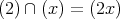 であることを示せ。
であることを示せ。
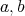 は整数とするとき,
は整数とするとき,
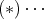
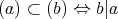 を証明せよ。
を証明せよ。
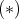 を用いて次を示せ:
を用いて次を示せ:

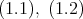 の逆の包含関係
の逆の包含関係
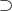 を示し,
を示し,
 を
を
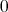 でない
でない
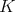 のイデアルとすると,
のイデアルとすると,
 は
は
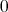 でない
でない
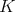 の元
の元
 を含むから,イデアルの定義により
を含むから,イデアルの定義により
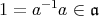 である。よって任意の
である。よって任意の
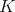 の元
の元
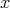 に対して,
に対して,
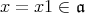 となり
となり
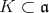 である。したがって,
である。したがって,
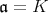 であるから,体
であるから,体
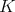 のイデアルは
のイデアルは
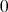 と
と
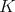 自身の 2 つである。
自身の 2 つである。
逆に可換環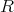 が
が
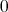 と
と
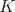 自身の 2 つしかイデアルをもたないとする。このとき,任意の
自身の 2 つしかイデアルをもたないとする。このとき,任意の
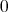 でない
でない
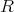 の元
の元
 に対し,
に対し,
 で生成されるイデアル
で生成されるイデアル
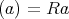 はゼロイデアルではないから,仮定によりこれは
はゼロイデアルではないから,仮定によりこれは
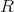 自身となる。したがって,
自身となる。したがって,
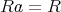 であるから,
であるから,
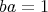 となるような
となるような
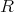 の元
の元
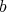 が存在するので,
が存在するので,
 は単数。今,
は単数。今,
 は任意の
は任意の
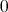 でない
でない
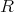 の元であったから,
の元であったから,
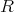 は体である。
は体である。

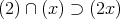 であること。
であること。
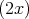 の任意の元は
の任意の元は
![2x ⋅ f(x) (f(x) ∈ Z [x ])](img/el2158x.gif) と表せるから,
と表せるから,
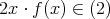 かつ
かつ
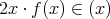 である。
である。
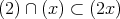 であること。
であること。
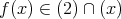 とし,
とし,
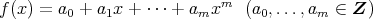 とおく。この
とき,
とおく。この
とき,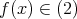 より,
より,
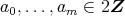 であり
であり
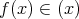 より,
より,
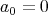 である。した
がって,
である。した
がって,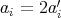 とおけば,
とおけば,
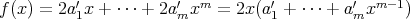 で
あるから
で
あるから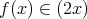 である。
である。

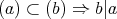
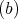 の任意の元は
の任意の元は
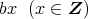 と表せる。今,
と表せる。今,
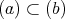 より,
より,
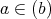 である
から,
である
から,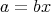 となるような
となるような
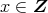 が存在するので,
が存在するので,
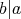 である。
である。
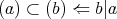
仮定から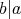 であるから
であるから
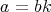 とおいておけば,任意の
とおいておけば,任意の
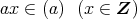 に
対して,
に
対して,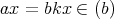 である。したがって,
である。したがって,
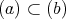 である。
である。
以上から,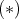 が証明された。
が証明された。
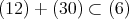 であること。
であること。
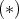 より,
より,
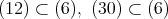 である。
である。
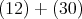 は
は
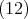 と
と
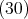 を含む最小のイデアルであるから,
を含む最小のイデアルであるから,
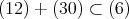 である。
である。
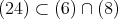 であること。
であること。
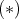 より,
より,
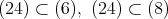 であるから,任意の
であるから,任意の
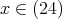 に対して
に対して
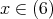 かつ
かつ
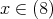 である。したがって,
である。したがって,
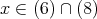 より,
より,
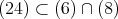 である。
である。

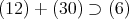 であること。
であること。
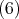 の任意の元
の任意の元
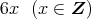 が,
が,
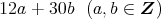 の形に表せることを示せばよ
い。
の形に表せることを示せばよ
い。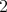 と
と
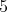 は互いに素であるから,
は互いに素であるから,
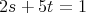 となるような整数
となるような整数
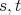 が存在する。したがって,
が存在する。したがって,
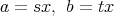 とおけば,
とおけば,
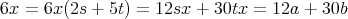 となる。
となる。
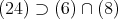 であること。
であること。
任意の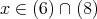 に対して,
に対して,
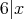 かつ
かつ
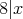 であるから,
であるから,
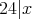 である。
である。
