環論演習2
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
- (1)教科書 問題 2.1,問2
「![f(x) ∈ R [x], a ∈ R](img/el259x.gif) とする。このとき,
とする。このとき,
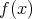 が既約
が既約
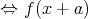 が既約」を
示せ。
が既約」を
示せ。
- (2)(1) を利用し,素数
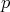 に対して,
に対して,
が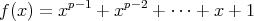
![Z [x]](img/el264x.gif) の多項式として既約であることを示せ。
の多項式として既約であることを示せ。
問 2.
![f (x) ∈ Q[x]](img/el265x.gif) は次数 3 の多項式とする。
は次数 3 の多項式とする。命題 「
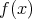 が
が
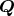 の中に根を持たないならば,
の中に根を持たないならば,
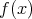 は既約」
は既約」を証明せよ。次に,この命題の逆を書き,証明せよ。
![f(x) ∈ R [x], a ∈ R](img/el259x.gif) とする。このとき,
とする。このとき,
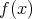 が既約
が既約
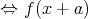 が既約」を
示せ。
が既約」を
示せ。
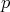 に対して,
に対して,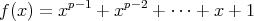
![Z [x]](img/el264x.gif) の多項式として既約であることを示せ。
の多項式として既約であることを示せ。
![f (x) ∈ Q[x]](img/el265x.gif) は次数 3 の多項式とする。
は次数 3 の多項式とする。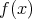 が
が
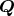 の中に根を持たないならば,
の中に根を持たないならば,
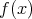 は既約」
は既約」
対偶をとり,「
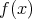 が可約
が可約
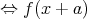 が可約」であることを示す。
が可約」であることを示す。
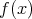 が既約でないとすれば,
が既約でないとすれば,
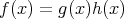 となるような,
となるような,
![g(x),h(x) ∈ R [x]](img/el273x.gif) (ただし
(ただし
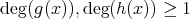 )が存在する。このとき,
)が存在する。このとき,
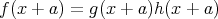 であり,
であり,
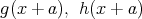 はいずれも次数 1 以上であるから
はいずれも次数 1 以上であるから
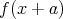 は可約である。
逆に,
は可約である。
逆に,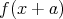 が可約ならば上の結果から,
が可約ならば上の結果から,
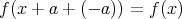 は可約である。
は可約である。

3次の多項式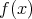 が可約であるとし,
が可約であるとし,
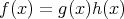 であるとすれば,
であるとすれば,
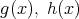 の
いずれかの次数は 1 でなくてはならない。それを
の
いずれかの次数は 1 でなくてはならない。それを
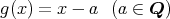 とすれば,
とすれば,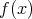 は
は を根に持つ。したがって,
を根に持つ。したがって,
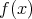 が
が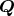 の中に根を持たないならば,
の中に根を持たないならば,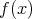 は既約
である。
は既約
である。

逆:「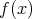 が既約ならば
が既約ならば
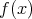 は
は
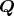 の中に根を持たない」
の中に根を持たない」
もし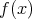 が
が
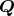 の中に根
の中に根
 をもてば
をもてば
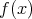 は
は
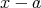 で割り切れるから,
で割り切れるから,
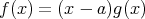 と表せる。今,
と表せる。今,
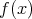 の次数は 3 であるから,
の次数は 3 であるから,
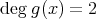 であり,
であり,
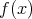 は可約である。
は可約である。
