環論演習1
理学部 数理・自然情報科学科 西田憲司演習問題
問1.
-
環
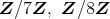 の単数を求めよ。
の単数を求めよ。
- 環
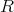 の元
の元
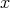 が,ある正整数
が,ある正整数
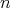 に対し,
に対し,
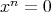 を充たすとき,ベキ零という。
を充たすとき,ベキ零という。
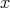 がベキ零ならば
がベキ零ならば
 は単数であることを示せ。
は単数であることを示せ。
問2.
例12の環
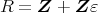 に対し,単数の全体
に対し,単数の全体
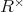 を求めよ。
を求めよ。
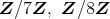 の単数を求めよ。
の単数を求めよ。
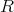 の元
の元
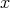 が,ある正整数
が,ある正整数
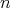 に対し,
に対し,
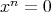 を充たすとき,ベキ零という。
を充たすとき,ベキ零という。 がベキ零ならば
がベキ零ならば
 は単数であることを示せ。
は単数であることを示せ。
例12の環
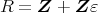 に対し,単数の全体
に対し,単数の全体
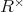 を求めよ。
を求めよ。
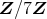 について
について
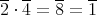 であるから
であるから
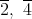 は単数である。同様に,
は単数である。同様に,
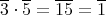 であるから
であるから
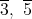 は単数であり,
は単数であり,
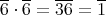 であるから
であるから
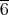 もまた単数である。単位元
もまた単数である。単位元
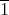 はもちろん単数。
はもちろん単数。
したがって,
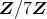 の単数は
の単数は
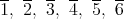 である。
である。
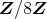 について
について
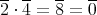 より,
より,
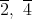 は零因子なので単数ではない。
は零因子なので単数ではない。
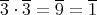 であるから,
であるから,
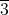 は単数である。
は単数である。
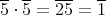 であるから,
であるから,
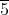 は単数である。
は単数である。
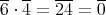 より,
より,
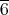 は零因子なので単数ではない。
は零因子なので単数ではない。
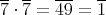 より,
より,
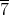 は単数である。以上から,
は単数である。以上から,
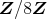 の単数は
の単数は
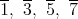 である。
である。
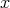 がベキ零ならば,
がベキ零ならば,
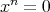 をみたすような
をみたすような
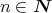 が存在する。このとき,
が存在する。このとき,
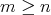 なる任意の
なる任意の
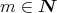 に対して
に対して
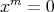 であるから,そのような
であるから,そのような
 を奇数としてとれば,
を奇数としてとれば,
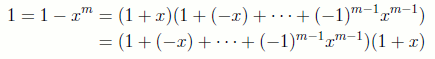
 は単数である。
は単数である。

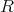 の単位元は1である。実際任意に
の単位元は1である。実際任意に
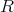 の元
の元
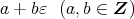 をとれば,
をとれば,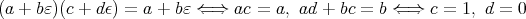
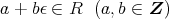 を単数とし,
を単数とし,
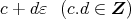 をその逆元とすると,
をその逆元とすると,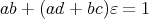 であるから,
であるから,
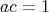 かつ
かつ
 である。今,
である。今,
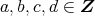 で
あるから,
で
あるから,
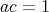 より
より
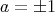 となる。逆に,
となる。逆に,
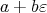 は
は
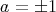 ならば,
ならば,
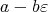 を逆元にもつような単数であることがわかるから,
を逆元にもつような単数であることがわかるから,
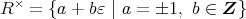 である。
である。