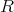 上に加法と乗法が定義されているとする。
上に加法と乗法が定義されているとする。
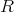 が環 (ring) であるとは
が環 (ring) であるとは
集合
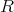 上に加法と乗法が定義されているとする。
上に加法と乗法が定義されているとする。
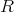 が環 (ring) であるとは
が環 (ring) であるとは
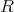 は加法に関して加群である。
は加法に関して加群である。
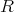 は乗法に関して半群である。
は乗法に関して半群である。
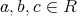 について
について
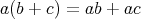 ,
,
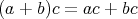 が成り立つ。
が成り立つ。
を満たすことをいう。更に
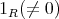 が存在する。
が存在する。
が成り立つとき、
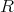 を単位元をもつ環という。
を単位元をもつ環という。
(R1), (R2), (R3) が成り立ち、かつ
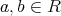 に対して
に対して
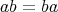 が成り立つ。
が成り立つ。
が満たされるとき
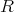 を可換環 (commutative ring) という。
を可換環 (commutative ring) という。
環
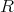 の加法に関する単位元を零元といい
の加法に関する単位元を零元といい
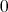 または
または
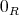 と書く。
と書く。
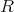 が単位元をもつ環であるとき、乗法に関する単位元を単に単位元といい
が単位元をもつ環であるとき、乗法に関する単位元を単に単位元といい
 または
または
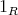 と書く。
と書く。
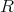 が単位元をもつ環のとき、
が単位元をもつ環のとき、
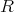 は乗法についてモノイドであるから、その単数群
は乗法についてモノイドであるから、その単数群
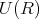 が考えられる。
が考えられる。
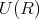 を環
を環
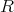 の単数群 (unit group) といい、その元を
の単数群 (unit group) といい、その元を
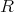 の正則元、または単数 (unit) という。 (正則元を扱うときには常に、考える環が単位元をもつと仮定する。)
の正則元、または単数 (unit) という。 (正則元を扱うときには常に、考える環が単位元をもつと仮定する。)
単位元をもつ環
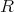 において、
において、
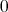 以外のすべての元が正則元であるとき
以外のすべての元が正則元であるとき
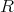 を斜体 (skewfield, division ring) という。特に可換な斜体を体 (field)、または可換体 (commutative field) という。
を斜体 (skewfield, division ring) という。特に可換な斜体を体 (field)、または可換体 (commutative field) という。
例3.1.4 (有理数体、実数体、複素数体).
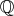 ,
,
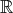 ,
,
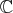 は通常の加法と乗法で体である。これをそれぞれ有理数体 (rational number field)、実数体 (real number field)、複素数体(complex number field) という。
は通常の加法と乗法で体である。これをそれぞれ有理数体 (rational number field)、実数体 (real number field)、複素数体(complex number field) という。
例3.1.5 (全行列環).
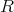 を (可換とは限らない) 環とする。
を (可換とは限らない) 環とする。
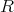 の元を成分とする
の元を成分とする
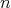 次正方行列の全体は通常の演算で環になる。これを
次正方行列の全体は通常の演算で環になる。これを
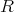 上
上
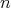 次の全行列環 (full matrixring) といい
次の全行列環 (full matrixring) といい
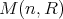 、または
、または
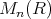 と書く。
と書く。
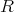 が単位元をもてば
が単位元をもてば
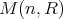 も単位元をもつ。
も単位元をもつ。
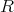 を環とする。
を環とする。
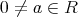 が
が
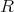 の左零因子 (left zero divisor) であるとは、ある
の左零因子 (left zero divisor) であるとは、ある
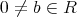 が存在して
が存在して
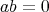 となることである。同様に
となることである。同様に
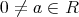 が
が
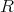 の右零因子(right zero divisor) であるとは、ある
の右零因子(right zero divisor) であるとは、ある
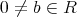 が存在して
が存在して
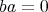 となることである。
となることである。
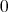 は左 (右) 零因子とはいわないことにする。
は左 (右) 零因子とはいわないことにする。
証明.
 を正則元であり、かつ左零因子であるとする。ある
を正則元であり、かつ左零因子であるとする。ある
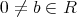 が存在して
が存在して
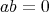 である。このとき
である。このとき
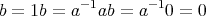
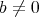 に矛盾する。
に矛盾する。

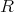 が可換環であるときには
が可換環であるときには
 が左零因子であることと、右零因子であることは同値であり、左右の区別をする必要がない。このとき
が左零因子であることと、右零因子であることは同値であり、左右の区別をする必要がない。このとき
 を単に零因子 (zero divisor) という。
を単に零因子 (zero divisor) という。
単位元をもつ可換環
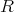 が整域 (integral domain) であるとは、
が整域 (integral domain) であるとは、
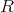 に零因子が存在しないことである。
に零因子が存在しないことである。
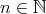 ,
,
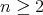 を一つ固定する。前と同じように
を一つ固定する。前と同じように
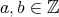 に対して、ある
に対して、ある
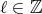 が存在して
が存在して
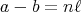 となるとき
となるとき
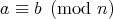 と書くことにする (問
1.2.1
)。このときこの関係は同値関係である。その
と書くことにする (問
1.2.1
)。このときこの関係は同値関係である。その
 を含む同値類は
を含む同値類は
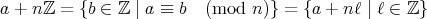
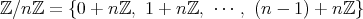
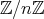 は加群
は加群
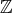 の部分加群
の部分加群
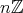 による剰余群で
による剰余群で
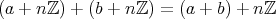
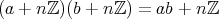
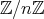 に乗法が矛盾なく定義できることを確認する。
に乗法が矛盾なく定義できることを確認する。
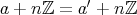 ,
,
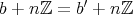 とする。ある
とする。ある
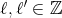 が存在して
が存在して
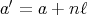 ,
,
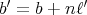 である。このとき
である。このとき
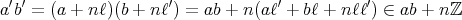
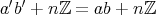 であり、乗法は矛盾なく定義される。
であり、乗法は矛盾なく定義される。
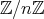 は加群であり、乗法については
は加群であり、乗法については
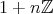 を単位元とするモノイドである。また分配法則、交換法則が成り立つことは容易に確かめられ、したがって
を単位元とするモノイドである。また分配法則、交換法則が成り立つことは容易に確かめられ、したがって
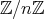 は可換環の構造を持つ。以下では文脈から
は可換環の構造を持つ。以下では文脈から
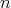 が明らかなときには
が明らかなときには
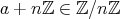 を
を
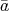 とも書くことにする。
とも書くことにする。
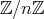 の単数、および零因子を考える。
の単数、および零因子を考える。
例3.2.1.
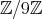 を考える。乗法に関する演算表は以下のようになる。
を考える。乗法に関する演算表は以下のようになる。

 を含むものが単数で、
を含むものが単数で、
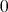 との積以外に
との積以外に
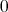 を含むものが零因子である。したがって単数群は
を含むものが零因子である。したがって単数群は
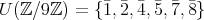 であり、零因子は
であり、零因子は
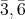 である。単数どうしの積は、また単数であることも確認しておこう。
である。単数どうしの積は、また単数であることも確認しておこう。
一般の場合を扱うために以下の定理を用意する。
証明.
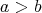 と仮定してかまわない。このとき
と仮定してかまわない。このとき
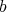 に関する帰納法で示す。
に関する帰納法で示す。
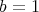 ならば
ならば
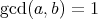 で
で
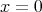 ,
,
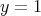 とすればよい。
とすればよい。
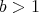 とする。
とする。
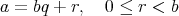
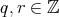 が存在する。
が存在する。
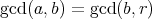 であることを示す。
であることを示す。
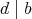 とする。このとき
とする。このとき
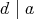 ならば
ならば
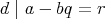 である。また
である。また
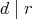 ならば
ならば
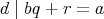 である。よって
である。よって
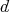 が
が
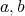 の公約数であることと
の公約数であることと
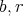 の公約数であることは同値である。したがって
の公約数であることは同値である。したがって
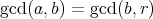 が成り立つ。
が成り立つ。
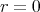 ならば
ならば
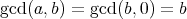 で
で
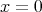 ,
,
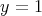 とすればよい。
とすればよい。
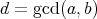 とおく。
とおく。
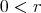 とすれば
とすれば
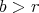 なので
なので
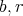 に帰納法の仮定を適用することができ、ある
に帰納法の仮定を適用することができ、ある
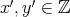 が存在して
が存在して
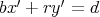 となる。このとき
となる。このとき
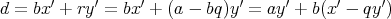
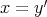 ,
,
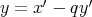 とおけばよい。
とおけばよい。

この定理を用いて、一般の
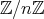 の単数を決定することができる。
の単数を決定することができる。
証明.
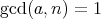 とする。このとき定理
3.2.2
より、ある
とする。このとき定理
3.2.2
より、ある
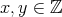 が存在して
が存在して
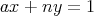 である。この両辺を
である。この両辺を
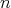 を法として考えれば
を法として考えれば
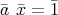 となり
となり
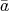 は単数である。
は単数である。
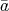 が単数であるとする。ある
が単数であるとする。ある
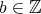 が存在して
が存在して
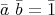 である。したがって
である。したがって
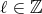 が存在して
が存在して
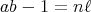 である。変形して
である。変形して
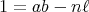 を得る。この式の右辺は
を得る。この式の右辺は
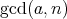 で割り切れるので、左辺の
で割り切れるので、左辺の
 も
も
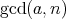 で割り切れ
で割り切れ
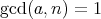 となる。
となる。

次に
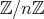 の零因子を決定しよう。
の零因子を決定しよう。
証明. (2)
 (3) は定理
3.2.3
で示されている。零因子は単数ではないので (1)
(3) は定理
3.2.3
で示されている。零因子は単数ではないので (1)
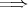 (2) も成り立つ。
(2) も成り立つ。
(3)
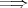 (1)
(1)
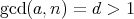 とする。このとき
とする。このとき
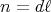 とすれば
とすれば
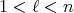 となる。
となる。
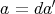 とすれば
とすれば
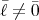 であって
であって
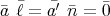 となる。よって
となる。よって
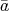 は零因子である。
は零因子である。

証明. 前の定理より (1)
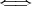 (2) が成り立つ。
(2) が成り立つ。
(3)
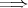 (1)
(1)
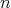 が素数ならば、任意の
が素数ならば、任意の
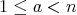 に対して
に対して
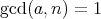 であるから
であるから
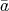 は単数であり
は単数であり
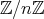 は体である。
は体である。
(1)
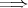 (3)
(3)
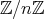 が体ならば、任意の
が体ならば、任意の
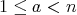 に対して
に対して
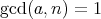 でなくてはならず
でなくてはならず
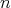 は素数である。
は素数である。

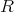 を環とする。
を環とする。
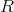 の部分集合
の部分集合
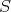 が
が
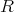 の部分環 (subring) であるとは
の部分環 (subring) であるとは
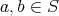 ならば
ならば
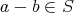 ,
,
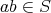 である。
である。
を満たすこととする。
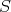 が
が
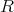 の部分環であるとき
の部分環であるとき
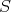 自身は環である。
自身は環である。
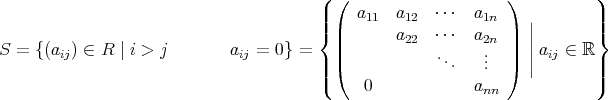
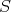 は
は
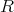 の部分環であることを確認する。
の部分環であることを確認する。
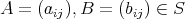 とする。
とする。
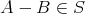 は明らかであるから
は明らかであるから
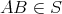 を示せばよい。
を示せばよい。
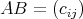 とおくと
とおくと
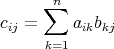
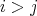 とする。
とする。
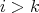 ならば
ならば
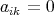 で
で
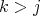 ならば
ならば
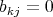 である。よって
である。よって
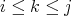 のときのみ
のときのみ
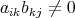 となり得るが
となり得るが
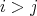 であるから、すべての
であるから、すべての
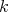 に対して
に対して
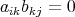 であり
であり
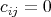 となる。よって
となる。よって
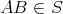 である。
である。
この例の
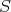 が環になることを定義から直接示すのは、いろいろな条件を満たすことを確かめなければならず、なかなか大変である。しかし
が環になることを定義から直接示すのは、いろいろな条件を満たすことを確かめなければならず、なかなか大変である。しかし
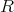 の部分集合で、その演算も
の部分集合で、その演算も
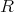 の演算を用いて定義されているため、部分環であることを示しさえすれば
の演算を用いて定義されているため、部分環であることを示しさえすれば
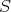 自身が環であることを示すことができる。一般の場合にも、ある集合がある演算で環になることを示したいときには、それが良く知られた環の部分集合として得られていないかどうかを考えることが有効であることが多い。
自身が環であることを示すことができる。一般の場合にも、ある集合がある演算で環になることを示したいときには、それが良く知られた環の部分集合として得られていないかどうかを考えることが有効であることが多い。
群
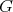 とその正規部分群
とその正規部分群
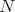 に対して、剰余群
に対して、剰余群
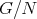 を定義することができた。同様に、環
を定義することができた。同様に、環
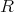 のその “ある性質” を満たす部分集合
のその “ある性質” を満たす部分集合
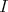 に対して、剰余環
に対して、剰余環
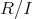 を定義することを考える。どのような性質を持つ
を定義することを考える。どのような性質を持つ
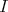 に対して剰余環は定義できるのであろうか。
に対して剰余環は定義できるのであろうか。
多くの場合、数学のテキストや講義では、まずある概念の定義を与え、その後 でいろいろな性質などを学ぶ。しかし実際には後の議論がうまくいくように定 義を行っているのであり、思考の順序と学ぶ順序は逆になっている。ここでは どの様な思考から定義が行われるのかを見てみよう。
まず、
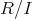 を定義するために同値関係が必要である。そこで
を定義するために同値関係が必要である。そこで
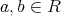 に対して、関係
に対して、関係
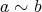 を
を
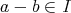 となることで定め、
となることで定め、
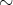 が同値関係になるための条件を考える。
が同値関係になるための条件を考える。
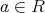 に対して
に対して
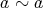 となるためには
となるためには
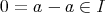 が必要十分であ る。
が必要十分であ る。
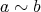 ならば
ならば
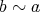 」が成り立つためには「
」が成り立つためには「
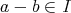 なら ば
なら ば
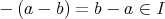 」となることが必要十分で、さらにこれは「
」となることが必要十分で、さらにこれは「
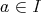 なら ば
なら ば
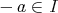 」となることと同値である。
」となることと同値である。
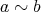 ,
,
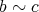 ならば
ならば
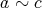 」が成り立つには「
」が成り立つには「
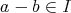 ,
,
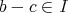 ならば
ならば
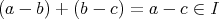 」となることが必要十分で、さらにこれは「
」となることが必要十分で、さらにこれは「
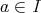 ,
,
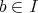 ならば
ならば
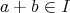 」となることと同値である。
」となることと同値である。
以上より
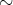 が同値関係になることと
が同値関係になることと
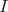 が
が
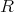 の部分加群であることは同値である。これによって同値類の集合
の部分加群であることは同値である。これによって同値類の集合
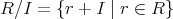 が考えられる。
が考えられる。
 を
を
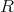 の部分加群とし、
の部分加群とし、
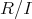 における演算を
における演算を
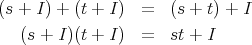
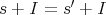 ,
,
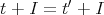 とする。
とする。
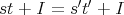 となる条件を考えれば よい。ある
となる条件を考えれば よい。ある
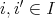 が存在して
が存在して
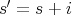 ,
,
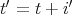 である。このとき
である。このとき
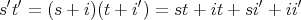
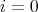 とすれば
とすれば
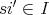 でなければならない。
でなければならない。
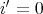 とすれば
とすれば
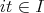 でなければならない。よって乗法が矛盾なく定義されるためには「
でなければならない。よって乗法が矛盾なく定義されるためには「
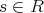 ,
,
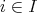 ならば
ならば
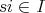 」かつ「
」かつ「
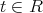 ,
,
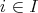 ならば
ならば
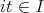 」が成り立つことが必要十分 である。
」が成り立つことが必要十分 である。
以上より、
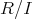 に加法と乗法が矛盾なく定義されるためには
に加法と乗法が矛盾なく定義されるためには
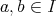 ならば
ならば
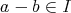 である。
である。
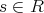 ,
,
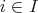 ならば
ならば
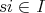 である。
である。
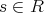 ,
,
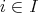 ならば
ならば
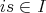 である。
である。
が成り立つことが必要十分である。乗法に関する結合法則、左右の分配法則が成り立つことは容易に確かめられ
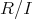 は環になる。これを
は環になる。これを
 の
の
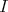 による剰余環 (factor ring) という。またこのとき
による剰余環 (factor ring) という。またこのとき
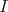 を
を
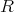 のイデアル (ideal) という。 (I1), (I2) を満たす集合
のイデアル (ideal) という。 (I1), (I2) を満たす集合
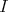 は左イデアル (left ideal)とよばれ、 (I1), (I3) を満たす集合
は左イデアル (left ideal)とよばれ、 (I1), (I3) を満たす集合
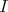 は右イデアル (right ideal) とよばれる。
イデアルを左 (右) イデアルと区別するために両側イデアル (two-sided ideal) ともいう。
は右イデアル (right ideal) とよばれる。
イデアルを左 (右) イデアルと区別するために両側イデアル (two-sided ideal) ともいう。
環
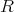 において、
において、
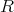 自身と
自身と
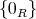 は
は
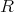 のイデアルである。これを
のイデアルである。これを
 の自明なイデアル (trivial ideal) という。
の自明なイデアル (trivial ideal) という。
 を可換環とする。
を可換環とする。
 の元を係数とする文字
の元を係数とする文字
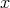 の整式
の整式
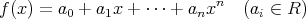
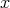 に関する
に関する
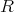 上の多項式 (polynomial) という。
上の多項式 (polynomial) という。
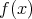 を単に
を単に
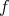 とも書く。
とも書く。
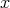 を不定元(indeterminate) または変数という。不定元
を不定元(indeterminate) または変数という。不定元
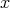 に関する
に関する
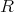 上の多項式全体の集合を
上の多項式全体の集合を
![R [x]](img/alg1507x.gif) と書く。
と書く。
![R[x]](img/alg1508x.gif) における加法と乗法を通常の場合と同じように定義する。すなわち、加法は
における加法と乗法を通常の場合と同じように定義する。すなわち、加法は

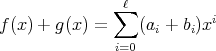
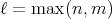 で、定義されていない係数は
で、定義されていない係数は
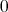 とする。また乗法は
とする。また乗法は
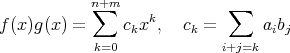
![R [x]](img/alg1514x.gif) は可換環となる。これを
は可換環となる。これを
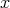 に関する
に関する
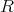 上の多項式環 (polynomialring) という。
上の多項式環 (polynomialring) という。
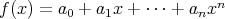 において
において
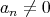 のとき、
のとき、
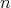 を
を
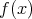 の次数 (degree) といい
の次数 (degree) といい
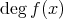 または
または
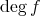 と書く。
と書く。
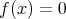 のときには、形式的に
のときには、形式的に
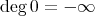 とする。非負整数
とする。非負整数
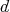 、または
、または
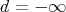 に対して
に対して
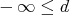 ,
,
 とする。
とする。
以下では
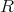 を整域とする。
を整域とする。
![f(x ), g(x) ∈ R [x ]](img/alg1530x.gif) に対して
に対して
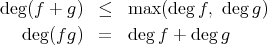
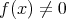 ,
,
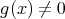 ならば
ならば
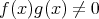 であり、
であり、
![R[x]](img/alg1535x.gif) は整域である。
は整域である。
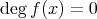 である
である
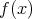 、または
、または
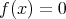 は
は
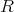 の元と思うことができ、これによって
の元と思うことができ、これによって
![R ⊂ R [x ]](img/alg1540x.gif) とみなす。
とみなす。
証明.
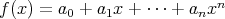 ,
,
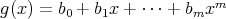 と する。まず
と する。まず
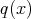 ,
,
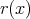 の存在を
の存在を
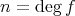 に関する帰納法で示す。
に関する帰納法で示す。
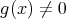 であるから
であるから
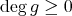 である。
である。
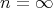 、または
、または
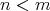 のときは
のときは
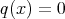 ,
,
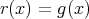 とすればよい。
とすればよい。
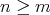 とする。
とする。
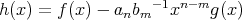 とおくと
とおくと
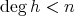 で、帰納法の仮定より
で、帰納法の仮定より
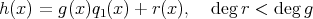
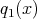 ,
,
![r(x) ∈ R [x]](img/alg1566x.gif) が存在する。このとき
が存在する。このとき
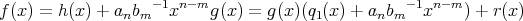
次に一意性を示す。
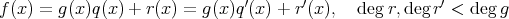
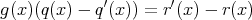
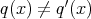 であるならば、左辺の次数は
であるならば、左辺の次数は
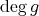 以上であり、右辺の次数は
以上であり、右辺の次数は
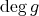 未満である。これは矛盾なので
未満である。これは矛盾なので
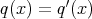 、よって
、よって
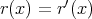 も成り立ち記述の一意性が示される。
も成り立ち記述の一意性が示される。

この定理は特に
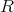 が体であるとき、
が体であるとき、
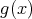 の最高次係数が
の最高次係数が
 であるとき、
であるとき、
に適用できる。最高次係数が
 である多項式をモニック (monic) な多項式という。
である多項式をモニック (monic) な多項式という。
定理
3.5.2
の
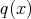 ,
,
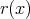 を、それぞれ
を、それぞれ
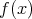 を
を
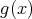 で割ったときの商、余りという。特に
で割ったときの商、余りという。特に
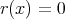 のとき
のとき
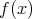 は
は
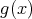 で割り切れるといい
で割り切れるといい
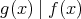 と書く。
と書く。
![nf(x) = a0 + a1x + ⋅⋅⋅ + anx ∈ R[x]](img/alg1587x.gif) と
と
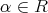 に対して
に対して
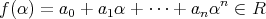
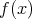 に
に
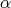 を代入した値という。
を代入した値という。
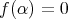 であるとき
であるとき
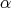 は
は
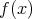 の根 (root) であるという。
の根 (root) であるという。
証明.
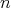 に関する帰納法で示す。
に関する帰納法で示す。
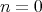 のときは
のときは
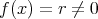 で、根は
で、根は
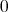 個である。よって命題は成り立つ。
個である。よって命題は成り立つ。
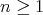 とする。
とする。
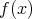 に根が存在しなければ命題は成立する。よって
に根が存在しなければ命題は成立する。よって
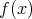 に根が存在すると仮定してよく、
に根が存在すると仮定してよく、
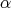 を一つの根とする。このとき
を一つの根とする。このとき
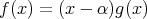
![g (x ) ∈ R [x]](img/alg1623x.gif) が存在し
が存在し
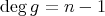 である。帰納法の仮定より
である。帰納法の仮定より
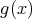 の根は高々
の根は高々
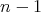 である。
である。
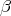 を
を
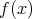 の根とすれば
の根とすれば
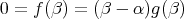
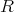 が整域であることから
が整域であることから
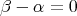 または
または
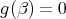 である。これは
である。これは
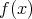 の根が
の根が
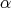 であるか、または
であるか、または
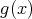 の根であることを意味し、よって
の根であることを意味し、よって
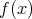 の根は高々
の根は高々
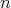 個である。
個である。

証明.
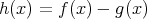 とおく。
とおく。
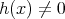 ならば
ならば
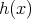 は高々
は高々
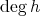 個の根をもつ。よって
個の根をもつ。よって
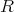 が無限個の元を含むならば
が無限個の元を含むならば
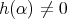 となる
となる
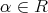 が存在する。よって
が存在する。よって
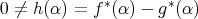 であり
であり
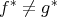 である。
である。

多変数の多項式環
![R [x1,x2,⋅⋅⋅ ,xn ]](img/alg1661x.gif) は帰納的に
は帰納的に
![R [x1, x2,⋅⋅⋅ ,xn] = R [x1, x2,⋅⋅⋅ ,xn- 1][xn]](img/alg1662x.gif)
![R [x1, ⋅⋅⋅ ,xn- 1]](img/alg1663x.gif) 上の変数
上の変数
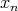 に関する多項式環) として定義される。その元は
に関する多項式環) として定義される。その元は
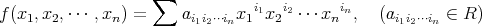
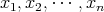 に関する
に関する
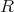 上の多項式 (polynomial) という。
上の多項式 (polynomial) という。
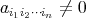 のとき
のとき
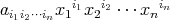 を
を
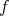 の項 (term) といい
の項 (term) といい
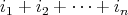 をその次数(degree) という。
をその次数(degree) という。
証明.
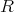 が整域だから
が整域だから
![R[x1]](img/alg1676x.gif) は整域、よって
は整域、よって
![R [x1,x2] = R[x1][x2 ]](img/alg1677x.gif) も整域、これを繰り返して
も整域、これを繰り返して
![R [x1,x2,⋅⋅⋅ ,xn]](img/alg1678x.gif) も整域である。
も整域である。
![U(R ) = U (R [x])](img/alg1679x.gif) を示せば、上と同じような議論で
を示せば、上と同じような議論で
![R[x ,x ,⋅⋅⋅ ,x ] 1 2 n](img/alg1680x.gif) の単数は
の単数は
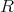 の単数と一致する。
の単数と一致する。
![f(x) ∈ R [x ]](img/alg1682x.gif) を単数とする。ある
を単数とする。ある
![g (x ) ∈ R [x]](img/alg1683x.gif) が存在して
が存在して
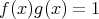 である。次数を比べると
である。次数を比べると
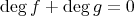 であるから
であるから
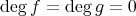 、すなわち
、すなわち
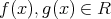 である。よって
である。よって
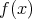 は
は
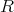 の単数であり
の単数であり
![U (R [x ]) ⊂ U (R)](img/alg1690x.gif) である。
である。
![U(R ) ⊂ U (R[x])](img/alg1691x.gif) は明らかであり
は明らかであり
![U (R) = U (R[x])](img/alg1692x.gif) である。
である。

証明. (1)
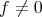 ならば
ならば
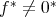 であることを示せばよい。これを
であることを示せばよい。これを
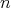 に関する帰納法で示す。
に関する帰納法で示す。
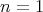 のときは既に示した。
のときは既に示した。
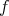 を
を
![R [x1,⋅⋅⋅ ,xn -1]](img/alg1710x.gif) を係数とする
を係数とする
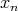 の多項式と見て
の多項式と見て
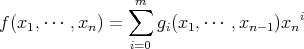
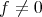 だから、ある
だから、ある
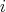 について
について
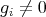 である。帰納法の仮定より
である。帰納法の仮定より
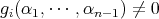 となる
となる
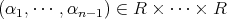 が存在する。このとき
が存在する。このとき
![0 ⁄= f (α1,⋅⋅⋅ ,αn -1,xn) ∈ R [xn ]](img/alg1718x.gif) であるから、ある
であるから、ある
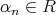 が存在して
が存在して
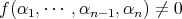 である。よって
である。よって
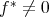 である。
である。
(2)
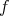 が条件を満たせば
が条件を満たせば
 は
は
 のすべての点で
のすべての点で
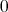 となる。よって (1) より
となる。よって (1) より
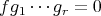 である。
である。
![R [x1,⋅⋅⋅ ,xn ]](img/alg1727x.gif) が整域で
が整域で
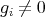 であるから
であるから
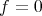 である。
である。

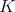 を体とする。
を体とする。
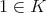 に対して
に対して
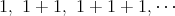
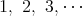 と書く。
と書く。
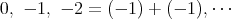 も考えて
も考えて
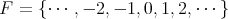
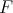 は
は
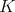 の部分環となる。
の部分環となる。
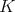 には零因子がないので
には零因子がないので
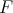 にも零因子はなく
にも零因子はなく
 は整域である。
は整域である。
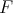 は加群として
は加群として
 で生成される巡回群で、したがって
で生成される巡回群で、したがって
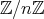 (
(
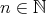 )、または
)、または
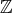 と本質的に同じものである (命題
2.3.9
)。これを同一視する。
と本質的に同じものである (命題
2.3.9
)。これを同一視する。
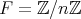 であるとき
であるとき
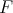 が整域であることにより
が整域であることにより
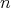 は素数になる (定理
3.2.5
)。この素数を
は素数になる (定理
3.2.5
)。この素数を
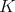 の標数(characteristic) という。
の標数(characteristic) という。
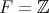 のときには
のときには
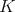 の標数は
の標数は
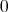 であるという。標数
であるという。標数
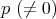 の体において
の体において
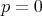 である。標数が
である。標数が
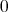 でない体を正標数の体ともいう。
でない体を正標数の体ともいう。
証明. 二項定理により
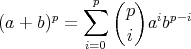 である。ここで
である。ここで
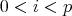 とすると
とすると
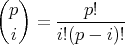
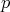 が現れるが分母には
が現れるが分母には
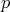 は現れない。よって、これは
は現れない。よって、これは
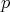 の倍数であり
の倍数であり
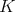 において
において
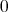 である。
である。

例3.6.5 (有理数体
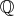 の構成). 有理整数環
の構成). 有理整数環
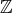 から有理数体
から有理数体
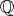 を構成しよう。
を構成しよう。
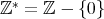 (非零因子全体の集合) とする。直積集合
(非零因子全体の集合) とする。直積集合
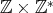 に関係
に関係
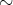 を「
を「
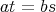 のとき
のとき
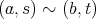 」として定める。この関係は同値関係である。
」として定める。この関係は同値関係である。
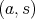 を含む同値類を
を含む同値類を
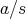 と書くことにする。同値類全体の集合
と書くことにする。同値類全体の集合
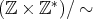 を
を
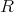 と書くことにする。
と書くことにする。
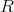 に加法と乗法を
に加法と乗法を
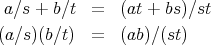
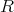 は可換環となる。単位元は
は可換環となる。単位元は
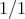 、零元は
、零元は
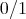 、
、
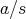 (
(
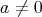 ) の逆元は
) の逆元は
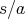 である。これにより
である。これにより
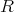 は体となる。この体を有理数体といい
は体となる。この体を有理数体といい
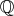 と書く。
と書く。
問3.6.6. 例 3.6.5 において以下のことを確認せよ。
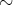 が同値関係であること。
が同値関係であること。
例
3.6.5
の構成は
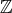 でなくても、一般の整域
でなくても、一般の整域
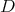 に対して行うことができる。このようにして作った体を整域
に対して行うことができる。このようにして作った体を整域
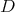 の商体 (quotient field) という。
の商体 (quotient field) という。
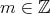 が平方数であるとは、
が平方数であるとは、
 となる
となる
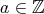 が存在することである。
が存在することである。
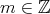 が平方自由 (square free) であるとは、
が平方自由 (square free) であるとは、
 であって
であって
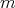 を割り切る
を割り切る
 以外の平方数が存在しないことである。
以外の平方数が存在しないことである。
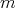 が平方自由であるということは、簡単に言えば
が平方自由であるということは、簡単に言えば
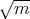 がより簡単な形に変形できないということである。
がより簡単な形に変形できないということである。
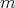 を平方自由な整数とし
を平方自由な整数とし
![√ -- √ -- ℚ [ m ] = {a + b m | a,b ∈ ℚ } √ -- { √ -- || }ℚ ( m ) = a-+-b√-m- ||a,b,c,d ∈ ℚ, c2 + d2 ⁄= 0 c + d m |](img/alg1840x.gif)
証明. まず
![√ --R = ℚ[ m ] ⊂ ℂ](img/alg1842x.gif) と見て、これが部分環であることを示す。
と見て、これが部分環であることを示す。
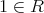 である。
である。
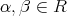 ならば
ならば
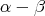 ,
,
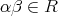 も明らかで、よって
も明らかで、よって
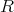 は可換環である。
は可換環である。
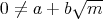 (
(
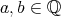 ) に 対 し て、 逆 元 が 存在することを示せばよい。
) に 対 し て、 逆 元 が 存在することを示せばよい。
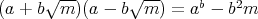 は
は
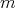 が平方自由なので
が平方自由なので
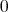 にはならない。
にはならない。
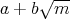 の逆元は
の逆元は
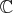 には存在するので、それが
には存在するので、それが
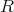 に含まれることをいえばよい。実際
に含まれることをいえばよい。実際
![√ ------1---- ------a---b--m-------- ---a----- ----b----√-- √ --a + b√m-- = (a + b√m--)(a - b√m--) = a2 - b2m - a2 - b2m m ∈ ℚ [ m]](img/alg1856x.gif)
![R = ℚ[√m--]](img/alg1857x.gif) は体である。
は体である。

![√ --ℚ[ m ]](img/alg1859x.gif) を二次体 (quadratic field) という。これは多項式環
を二次体 (quadratic field) という。これは多項式環
![ℚ [x]](img/alg1860x.gif) において
において
![(x2 - m )ℚ[x]](img/alg1861x.gif) というイデアルを考え、それによる剰余環
というイデアルを考え、それによる剰余環
![ℚ [x ]∕(x2 - m )ℚ [x]](img/alg1862x.gif) を考えていることと同じである。
を考えていることと同じである。
同様に
![f(x) ∈ ℚ [x]](img/alg1863x.gif) を既約多項式 (より小さい次数の多項式の積に分解しない多項式) とするとき、剰余環
を既約多項式 (より小さい次数の多項式の積に分解しない多項式) とするとき、剰余環
![ℚ [x]∕f(x )ℚ[x]](img/alg1864x.gif) は体となる。
このような体を代数体 (algebraic number field) という。
は体となる。
このような体を代数体 (algebraic number field) という。