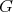 で
で
すべての元が正則元であるモノイドを群 (group) という。すなわち、演算の定義された集合
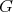 で
で
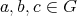 について
について
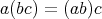 である。
である。
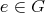 が存在して、任意の
が存在して、任意の
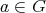 に対して
に対して
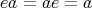 である。 (このとき
である。 (このとき
 を
を
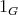 とも書く。)
とも書く。)
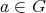 に対して、ある
に対して、ある
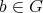 が存在して
が存在して
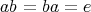 で ある。 (このときの
で ある。 (このときの
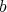 を
を
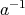 と書く。)
と書く。)
がすべて成り立つとき
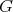 を群という。群は半群やモノイドの特別なものであるから、それらに対して成り立つことはすべて成り立つ。群
を群という。群は半群やモノイドの特別なものであるから、それらに対して成り立つことはすべて成り立つ。群
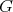 において、更に
において、更に
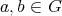 について
について
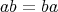 である。
である。
が成り立つとき
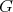 をアーベル群 (abelian group)、または可換群 (commutative group) という。
をアーベル群 (abelian group)、または可換群 (commutative group) という。
証明. (1)
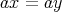 とすると、両辺に左から
とすると、両辺に左から
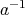 をかけて
をかけて
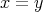 となる。逆も同様である。 (2)
となる。逆も同様である。 (2)
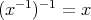 より
より
 となり
となり
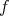 は全単射である。 (3)
は全単射である。 (3)
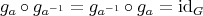 となり
となり
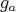 は全単射である。他も同様である。
は全単射である。他も同様である。

証明. 任意の
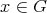 に対して
に対して
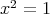 より
より
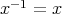 である。よって任意の
である。よって任意の
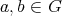 に対して
に対して
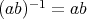 である。一方
である。一方
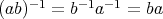 であるから
であるから
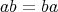 となる。
となる。

証明.
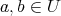 ならば
ならば
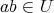 なので演算は
なので演算は
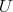 で定義される。また
で定義される。また
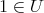 より
より
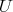 はモノイドである。
はモノイドである。
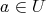 ならば
ならば
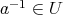 も成り立ち
も成り立ち
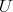 は群である。
は群である。

この命題の
 を
を
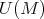 と書いて
と書いて
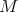 の単数群 (unit group) という。
の単数群 (unit group) という。
例2.1.7 (対称群). モノイド
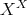 (例
1.7.5
) について、その単数群
(例
1.7.5
) について、その単数群
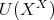 を
を
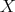 上の対称群 (symmetric group) といい、これを
上の対称群 (symmetric group) といい、これを
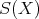 と書くことにする。
と書くことにする。
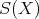 の元は
の元は
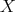 から
から
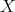 への全単射で、それを
への全単射で、それを
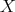 上の置換 (permutation) という。置換を具体的に書くには
上の置換 (permutation) という。置換を具体的に書くには
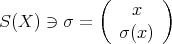
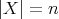 のとき、
のとき、
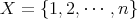 と考えても本質的には同じである。このとき
と考えても本質的には同じである。このとき
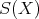 を
を
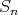 とも書き、これを
とも書き、これを
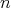 次対称群という。
次対称群という。
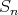 の元を
の元を
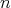 次の置換という。
次の置換という。
例2.1.8.
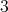 次対称群
次対称群
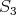 の元をすべて書くと以下のようになる。
の元をすべて書くと以下のようになる。

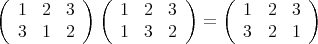
 については
については
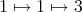 となる。逆元は上の行と下の行を入れ替えて
となる。逆元は上の行と下の行を入れ替えて
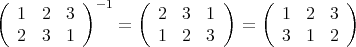
群
 について、
について、
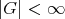 のとき
のとき
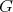 を有限群 (finite group) という。また
を有限群 (finite group) という。また
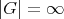 のとき
のとき
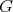 を無限群 (infinite group) という。
を無限群 (infinite group) という。
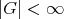 のとき
のとき
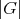 を
を
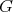 の位数 (order) という。
の位数 (order) という。
例2.1.12 (一般線形群).
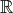 を成分とする
を成分とする
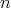 次正方行列の全体を
次正方行列の全体を
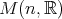 と書く。
と書く。
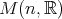 が行列の積によって単位行列を単位元とするモノイドである。その単数群を
が行列の積によって単位行列を単位元とするモノイドである。その単数群を
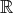 上
上
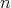 次の一般線形群 (general linear group) といい
次の一般線形群 (general linear group) といい
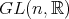 と書く。
と書く。
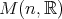 の単数は正則行列のことであるから
の単数は正則行列のことであるから
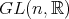 は正則行列全体の集合である。
は正則行列全体の集合である。
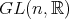 は無限群である。
は無限群である。
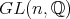 ,
,
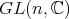 も同様である。
も同様である。
(これらは
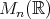 ,
,
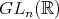 などとも書かれる。)
などとも書かれる。)
問2.1.14.
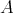 をモノイドで、集合として有限集合であるとする。右簡約法則「
をモノイドで、集合として有限集合であるとする。右簡約法則「
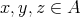 に対して
に対して
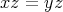 ならば
ならば
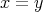 である」が成り立つとすると
である」が成り立つとすると
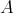 は群になる。これを示せ。また
は群になる。これを示せ。また
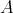 が有限集合ではないとき、これは正しくない。そのような例を具体的に一つ示せ。
が有限集合ではないとき、これは正しくない。そのような例を具体的に一つ示せ。
群
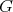 がアーベル群であるとき、その演算を加法の形で書くことが多い。このとき
がアーベル群であるとき、その演算を加法の形で書くことが多い。このとき
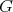 を加群(additive group)、または加法群という。
加群の単位元を零元といい
を加群(additive group)、または加法群という。
加群の単位元を零元といい
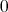 または
または
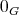 と書く。また
と書く。また
 の逆元は
の逆元は
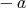 と書く。群の定義を加法の形で書き直すと以下のようになる。
と書く。群の定義を加法の形で書き直すと以下のようになる。
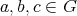 について
について
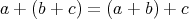 である。
である。
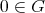 が存在して、任意の
が存在して、任意の
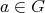 に対して
に対して
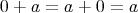 である。
である。
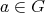 に対して、ある
に対して、ある
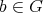 が存在して
が存在して
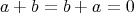 である。 (このときの
である。 (このときの
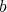 を
を
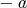 と書く。)
と書く。)
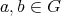 について
について
 である。
である。
加群
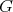 において
において
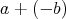 を
を
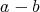 と書く。
と書く。
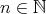 に対して、加群
に対して、加群
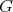 の元
の元
 を
を
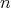 個加えたものを
個加えたものを
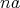 と書く。また
と書く。また
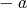 を
を
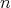 個加えたものを
個加えたものを
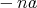 と書く。また
と書く。また
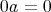 と定める。これによって任意の
と定める。これによって任意の
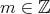 に対して
に対して
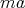 が定義され、以下が成り立つ。
が定義され、以下が成り立つ。
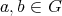 ,
,
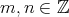 とする。
とする。
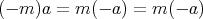 である。特に
である。特に
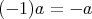 である。
である。
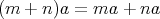
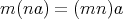
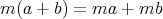
ここで (2), (3), (4) は通常の意味の分配法則、結合法則ではないことに注意する。
群
 の空でない部分集合
の空でない部分集合
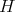 が
が
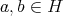 ならば
ならば
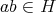 である。
である。
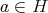 ならば
ならば
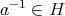 である。
である。
を満たすとき、
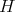 を
を
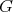 の部分群 (subgroup) という。
の部分群 (subgroup) という。
証明. (1)
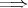 (2)
(2)
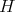 を
を
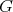 の部分群とする。 (B1) より
の部分群とする。 (B1) より
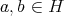 ならば
ならば
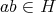 であるから
であるから
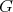 の演算は
の演算は
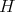 の演算を定義する。結合法則は
の演算を定義する。結合法則は
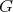 で成り立つので
で成り立つので
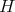 でも成り立つ。また
でも成り立つ。また
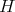 は空でないからある元
は空でないからある元
 を含む。このとき (B2) より
を含む。このとき (B2) より
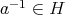 でもある。よって
でもある。よって
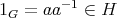 であり
であり
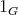 は
は
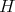 においても単位元である。 (B2)により任意の元の逆元も存在する。
においても単位元である。 (B2)により任意の元の逆元も存在する。
(2)
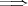 (3) 群の定義より明らかである。
(3) 群の定義より明らかである。
(3)
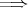 (1)
(1)
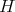 は空でないから
は空でないから
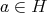 をとると
をとると
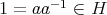 である。任意に
である。任意に
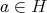 をとる。このとき
をとる。このとき
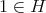 より
より
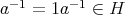 である。よって (B2) が成り立つ。最後に任意に
である。よって (B2) が成り立つ。最後に任意に
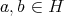 をとる。 (B2) より
をとる。 (B2) より
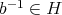 である。したがって
である。したがって
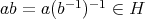 となり (B1) が成り立つ。
となり (B1) が成り立つ。

証明.
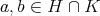 とする。
とする。
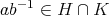 を示せばよい。
を示せばよい。
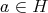 ,
,
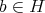 であるから
であるから
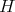 が部分群であることにより
が部分群であることにより
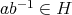 である。同様に
である。同様に
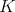 が部分群であることにより
が部分群であることにより
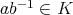 である。よって
である。よって
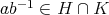 である。
である。

群
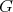 の部分集合
の部分集合
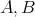 に対して
に対して
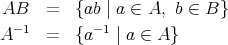
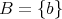 のときには
のときには
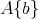 を
を
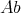 とも書く。
とも書く。
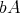 も同様である。
も同様である。
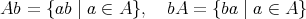
注意. 上記の計算を群の元の計算と混同してはいけない。例えば
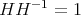 は一般に正しくない。 (なぜ正しくないのかを考えよ。)
は一般に正しくない。 (なぜ正しくないのかを考えよ。)
証明.
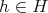 に対して
に対して
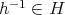 を示せばよい。
を示せばよい。
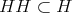 より
より
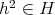 であり、同様にに繰り返せば、任意の
であり、同様にに繰り返せば、任意の
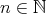 に対して
に対して
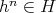 である。
である。
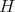 は有限集合であるから、すべての
は有限集合であるから、すべての
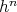 が異なることはできず、したがってある
が異なることはできず、したがってある
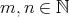 ,
,
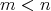 が存在して
が存在して
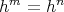 となる。このとき簡約法則によって
となる。このとき簡約法則によって
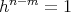 である。
である。
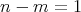 ならば
ならば
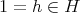 であり、
であり、
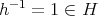 である。
である。
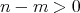 のとき
のとき
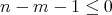 であって、よって
であって、よって
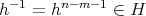 となる。
となる。

証明. (1)
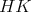 が
が
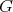 の部分群であるとする。このとき
の部分群であるとする。このとき
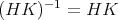 である。一方
である。一方
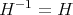 ,
,
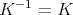 なので
なので
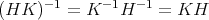 となるので
となるので
 となる。
となる。
次 に
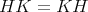 で あ る と する。このとき
で あ る と する。このとき
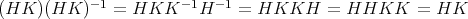 であるから
であるから
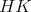 は
は
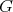 の部分群である。
の部分群である。
(2)
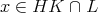 とする。
とする。
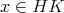 より
より
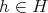 と
と
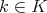 が存在して
が存在して
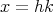 である。
である。
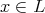 であって
であって
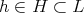 であるから
であるから
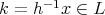 である。よって
である。よって
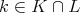 となり
となり
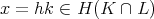 である。以上より
である。以上より
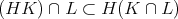 となる。
となる。
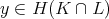 とする。ある
とする。ある
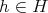 と
と
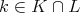 が存在して
が存在して
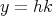 である。このとき
である。このとき
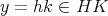 であり、
であり、
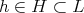 であるから
であるから
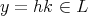 も成り立つ。よって
も成り立つ。よって
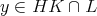 であり
であり
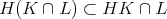 である。
である。
以上により
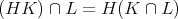 が成り立つ。
が成り立つ。

群
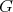 において
において
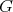 自身と
自身と
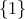 は
は
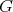 の部分群である。これらを
の部分群である。これらを
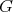 の自明な部分群(trivial subgroup) という。また
の自明な部分群(trivial subgroup) という。また
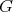 と異なる部分群を真部分群 (proper subgroup) という。
と異なる部分群を真部分群 (proper subgroup) という。
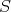 を群
を群
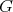 の部分集合とする。
の部分集合とする。
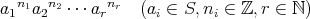
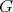 の部分群である。これを
の部分群である。これを
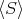 と書き、
と書き、
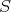 で生成される部分群(subgroup generated by
で生成される部分群(subgroup generated by
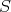 ) という。
) という。
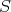 が有限集合
が有限集合
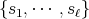 であるとき
であるとき
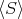 を
を
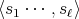 とも書く。
とも書く。
特に
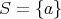 のとき
のとき
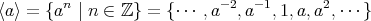
 で生成される巡回群 (cyclic group) といい
で生成される巡回群 (cyclic group) といい
 をその生成元 (generater) という。部分群
をその生成元 (generater) という。部分群
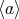 の位数を元
の位数を元
 の位数 (order) といい
の位数 (order) といい
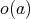 と書く。
と書く。
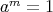 となる
となる
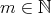 が存在すれば
が存在すれば
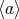 は有限巡回群である。
は有限巡回群である。
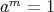 とな る
とな る
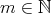 のうち最小のものを
のうち最小のものを
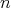 をすれば
をすれば
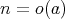 であって次が成り立 つ。
であって次が成り立 つ。
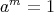
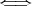
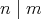
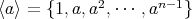 であって、これらの元はすべて相異なる。
であって、これらの元はすべて相異なる。
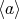 が無限巡回群ならば
が無限巡回群ならば
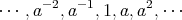
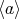 はこれらの元からなる。
はこれらの元からなる。
証明. (1) まず
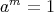 となる
となる
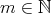 が存在すると仮定して (i)
が存在すると仮定して (i)
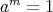
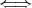
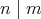 を示す。
を示す。
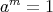 とすると
とすると
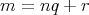 ,
,
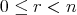 なる
なる
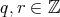 が存在する。このとき
が存在する。このとき
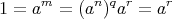
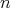 の最小性から
の最小性から
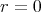 である。よって
である。よって
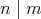 である。
である。
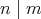 と仮定すれば、明らかに
と仮定すれば、明らかに
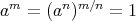 である。
である。
(i) より
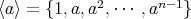 となることはすぐに分かる。これらがすべて異なることを示す。
となることはすぐに分かる。これらがすべて異なることを示す。
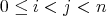 に対して
に対して
 とすると
とすると
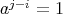 ,
,
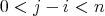 となり
となり
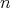 の最小性に反する。よってこれらはすべて異なり
の最小性に反する。よってこれらはすべて異なり
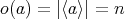 である。
である。
(2)
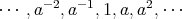 がすべて異なることを示せばよい。
がすべて異なることを示せばよい。
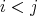 (
(
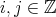 )に対して
)に対して
 と仮定すると、前と同様に
と仮定すると、前と同様に
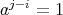 ,
,
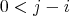 となり
となり
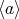 は有限巡回群になる。よって、これらの元はすべて異なる。
は有限巡回群になる。よって、これらの元はすべて異なる。

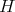 を群
を群
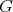 の部分群とする。
の部分群とする。
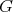 上の関係
上の関係
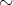 を「
を「
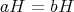 のとき
のとき
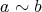 」で定める。このとき
」で定める。このとき
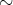 は
は
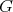 上の同値関係であることを示そう。
上の同値関係であることを示そう。
まず、任意の
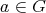 に対して
に対して
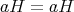 であるから
であるから
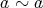 である。次に
である。次に
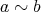 と仮定する。このとき
と仮定する。このとき
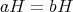 であるから
であるから
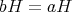 で
で
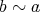 が成り立つ。
が成り立つ。
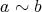 かつ
かつ
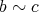 と仮定すれば
と仮定すれば
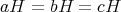 であるから
であるから
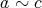 である。以上より
である。以上より
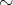 は同値関係である。
は同値関係である。
証明. (1)
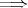 (2)
(2)
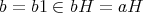 である。
である。
(2)
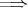 (3)
(3)
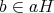 とすると、ある
とすると、ある
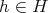 が存在して
が存在して
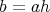 である。このとき
である。このとき
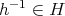 であるから
であるから
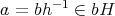 である。
である。
(3)
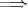 (4)
(4)
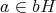 とすると、ある
とすると、ある
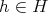 が存在して
が存在して
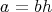 である。このとき
である。このとき
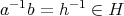 である。
である。
(4)
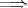 (1) ある
(1) ある
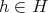 が存在して
が存在して
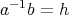 である。このとき
である。このとき
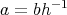 ,
,
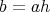 に注意しておく。
に注意しておく。
任意の
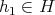 に対して
に対して
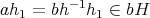 であるから
であるから
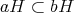 が成り立つ。任意の
が成り立つ。任意の
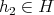 に対して
に対して
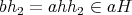 であるから
であるから
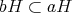 が成り立つ。以上より
が成り立つ。以上より
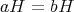 である。
である。

以上のことは関係
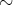 を
を
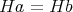 で定義しても同様に成り立つ。
で定義しても同様に成り立つ。
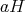 を
を
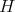 の左剰余類 (left coset) といい、左剰余類全体の集合を
の左剰余類 (left coset) といい、左剰余類全体の集合を
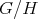 と書く。同様に
と書く。同様に
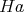 を
を
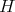 の右剰余類 (right coset) といい、右剰余類全体の集合を
の右剰余類 (right coset) といい、右剰余類全体の集合を
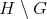 と書く。
と書く。
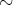 は同値関係で左剰余類はその同値類となるので、左剰余類に関する類別
は同値関係で左剰余類はその同値類となるので、左剰余類に関する類別
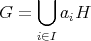
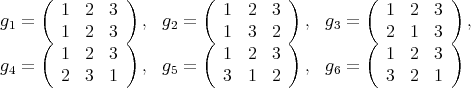
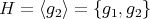 として左剰余類を考えてみると
として左剰余類を考えてみると
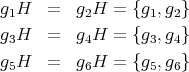
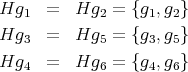
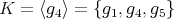 として左剰余類を考えてみると
として左剰余類を考えてみると
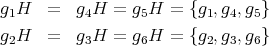
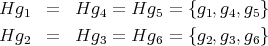
上の例のように、左剰余類による類別と右剰余類による類別が一致するとき、言い換えれば
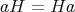 が任意の
が任意の
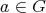 について成り立つとき、
について成り立つとき、
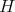 を
を
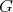 の正規部分群(normal subgroup) という。特に
の正規部分群(normal subgroup) という。特に
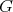 がアーベル群ならば任意の部分群は正規部分群である。
がアーベル群ならば任意の部分群は正規部分群である。
問2.4.4.
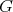 を有限群とし
を有限群とし
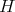 をその部分群とする。任意の
をその部分群とする。任意の
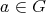 に対して
に対して
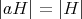 であることを示せ。また、異なる左剰余類の数を
であることを示せ。また、異なる左剰余類の数を
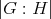 と書くとき
と書くとき
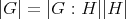 であることを示せ。 (これをLagrange の定理という。また
であることを示せ。 (これをLagrange の定理という。また
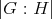 を
を
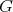 における
における
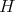 の指数 (index) という。右剰余類についても同様のことが成り立つ。)
の指数 (index) という。右剰余類についても同様のことが成り立つ。)
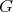 を群とし
を群とし
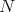 をその正規部分群とする。このとき、任意の
をその正規部分群とする。このとき、任意の
 について
について
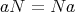 である。よって剰余類は右、左の区別をする必要がない。剰余類全体の集合
である。よって剰余類は右、左の区別をする必要がない。剰余類全体の集合
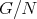 に以下のような演算を考える。
に以下のような演算を考える。
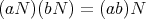
この場合
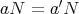 となる
となる
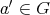 が存在するかもしれない。違う
が存在するかもしれない。違う
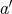 を使うと結果が変わってしまうというのでは演算 (写像) が定義されていると はいえない。したがって、演算が矛盾なく定義されるためには
を使うと結果が変わってしまうというのでは演算 (写像) が定義されていると はいえない。したがって、演算が矛盾なく定義されるためには
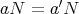 か つ
か つ
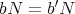 と仮定したとき
と仮定したとき
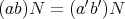 が成り立たなければならな い。
が成り立たなければならな い。
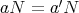 かつ
かつ
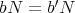 と仮定する。ある
と仮定する。ある
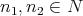 が存在して
が存在して
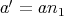 ,
,
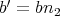 である。また
である。また
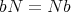 なので、ある
なので、ある
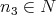 が存在して
が存在して
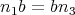 である。よってこのとき
である。よってこのとき
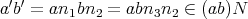
 である。よってこの演算は矛盾なく定義される。
である。よってこの演算は矛盾なく定義される。
この演算に関して、結合法則が成り立つことは明らかで、更に
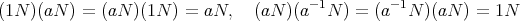
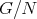 はこの演算によって
はこの演算によって
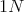 を単位元とする群になる。
を単位元とする群になる。
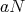 の逆元は
の逆元は
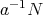 である。この群を
である。この群を
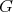 の
の
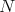 による剰余群 (factor group) といい、剰余類全体の集合と同じ記号を使って
による剰余群 (factor group) といい、剰余類全体の集合と同じ記号を使って
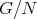 とかく。
とかく。