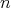 次元ベクトル全体の集合
次元ベクトル全体の集合
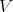 を考える。
を考える。
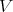 には加法や減法が定義される。しかし乗法、除法は定義されない。そこで “加法と減法が定義されている集合” についての一般論を構築しておけば、同様の性質をもつもの全てに適用できる。これが「群」である。 (この定義は正確ではないが、詳しくは後で学ぶ。)
には加法や減法が定義される。しかし乗法、除法は定義されない。そこで “加法と減法が定義されている集合” についての一般論を構築しておけば、同様の性質をもつもの全てに適用できる。これが「群」である。 (この定義は正確ではないが、詳しくは後で学ぶ。)
代数学、あるいはより広く数学、においては、ある対象のもつ基本的な性質のみに注目し、その性質だけを考えた理論を構築し、そこで得られた理論を元の問題に応用するといった手法がとられる。まったく違う対象が、類似の性質をもつ場合に、その共通の性質だけに注目して得られた結果は、そのどちらにも適用できる。したがって多くの対象がもつ性質を考え、それに関する一般論を構築しておけば、その適用範囲は広くなり、その重要性は増すことになる。このような考えから定義され、研究されてきたものに前述の「群」、「環」、「体」などがあるのである。
簡単な例を考えよう。例えば
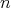 次元ベクトル全体の集合
次元ベクトル全体の集合
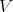 を考える。
を考える。
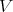 には加法や減法が定義される。しかし乗法、除法は定義されない。そこで “加法と減法が定義されている集合” についての一般論を構築しておけば、同様の性質をもつもの全てに適用できる。これが「群」である。 (この定義は正確ではないが、詳しくは後で学ぶ。)
には加法や減法が定義される。しかし乗法、除法は定義されない。そこで “加法と減法が定義されている集合” についての一般論を構築しておけば、同様の性質をもつもの全てに適用できる。これが「群」である。 (この定義は正確ではないが、詳しくは後で学ぶ。)
次に
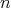 次の正方行列全体の集合
次の正方行列全体の集合
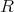 を考えよう。
を考えよう。
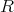 には加法と減法が定まっているので、これは群である。しかし
には加法と減法が定まっているので、これは群である。しかし
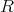 には乗法も定まっている。
には乗法も定まっている。
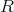 を単に加法に関する群と見ているだけでは、その乗法に関する情報は得られない。そこで加法、減法、乗法の定まっているものを「環」と定める。
を単に加法に関する群と見ているだけでは、その乗法に関する情報は得られない。そこで加法、減法、乗法の定まっているものを「環」と定める。
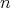 次正方行列には、一般に逆行列が存在するわけではないので、
次正方行列には、一般に逆行列が存在するわけではないので、
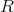 に除法を定めることはできない。しかしながら有理数全体、実数全体、複素数全体などのように除法も考えられるものも少なくはない。そこでこのように四則演算が行える対象を「体」と定めるのである。
に除法を定めることはできない。しかしながら有理数全体、実数全体、複素数全体などのように除法も考えられるものも少なくはない。そこでこのように四則演算が行える対象を「体」と定めるのである。
この講義ノートは主に「代数学, 永尾汎, 朝倉書店」[ 1] の第一章を参考にして作成したが、記号などはなるべく「代数学入門、石田信、実教出版」[ 2 ]に合わせた。
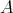 を集合 (set) とする。
を集合 (set) とする。
 が
が
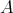 の要素 (element)、あるいは元、であることを
の要素 (element)、あるいは元、であることを
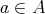 または
または
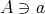 と書く。
と書く。
 が
が
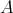 の要素でないことは
の要素でないことは
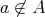 と書く。
と書く。
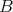 が
が
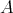 の部分集合 (subset) であるとき
の部分集合 (subset) であるとき
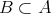 と書く。このとき
と書く。このとき
 も許すことに注意しておく。特に
も許すことに注意しておく。特に
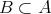 かつ
かつ
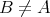 であるとき
であるとき
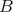 は
は
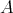 の真部分集合(proper subset) であるといい
の真部分集合(proper subset) であるといい
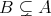 と書く。また空集合 (empty set) は
と書く。また空集合 (empty set) は
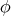 で表す。
で表す。
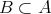 のとき
のとき
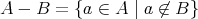 とする。
とする。
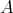 が有限集合 (finite set) であるとき、
が有限集合 (finite set) であるとき、
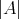 または
または
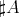 でその要素の個数を表す。
でその要素の個数を表す。
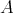 が無限集合 (infinite set) であるときには
が無限集合 (infinite set) であるときには
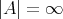 と書く。
と書く。
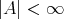 は
は
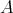 が有限集合であると言うことを意味するものとする。
が有限集合であると言うことを意味するものとする。
注意. 有限集合は、適当な非負整数
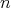 と、適当な番号付けによって
と、適当な番号付けによって
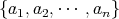 と書き表すことができる。しかし一般の無限集合を
と書き表すことができる。しかし一般の無限集合を
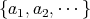 と書くのは誤りである。
と書くのは誤りである。
 ,
,
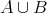 はそれぞれ共通部分 (intersection)、和集合 (union) である。一般に集合
はそれぞれ共通部分 (intersection)、和集合 (union) である。一般に集合
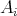 (
(
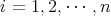 ) に対して
) に対して
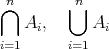
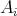 (
(
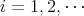 ) については
) については
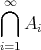 ,
,
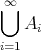 などの記号を用いるが、一般の無限集合については、適当な添字集合
などの記号を用いるが、一般の無限集合については、適当な添字集合
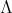 を用いて、集合を
を用いて、集合を
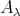 (
(
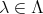 ) と表し、
) と表し、
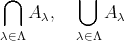
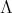 が有限集合でも用いることができるため、最も汎用的な記述である。
が有限集合でも用いることができるため、最も汎用的な記述である。
添字の動く範囲を適当に省略することも多い。例えば、全ての正の実数
 について、閉区間
について、閉区間
![[- a,a]](img/alg55x.gif) の共通部分を表すには、上記の規則に従えば
の共通部分を表すには、上記の規則に従えば
![⋂ [- a,a]a∈ {b∈ℝ|b>0}](img/alg56x.gif) と書くべきであるが、実際には省略して
と書くべきであるが、実際には省略して
![⋂ [- a,a ]a>0](img/alg57x.gif) などと書くことが多い。
などと書くことが多い。
和集合
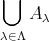 において
において
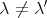 ならば
ならば
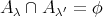 が成り立つとき、この和を共通部分をもたない和 (disjoint union) という。共通部分をもたない和
が成り立つとき、この和を共通部分をもたない和 (disjoint union) という。共通部分をもたない和
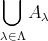 において
において
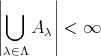 ならば、すべての
ならば、すべての
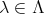 について
について
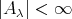 であり
であり
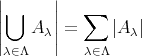 である。
<
である。
<
 と
と
 を集合とする。
を集合とする。
 の元と
の元と
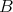 の元の順序対
の元の順序対
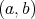 の全体からなる集合を
の全体からなる集合を
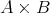 と書いて
と書いて
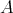 と
と
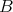 の直積集合 (direct product, cartesian product)、または単に直積という。
の直積集合 (direct product, cartesian product)、または単に直積という。
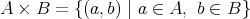
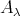 (
(
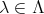 ) に対しても、各集合から一つずつ元を選び、それを元とする集合を定義し、これを直積集合という。このとき直積集合を
) に対しても、各集合から一つずつ元を選び、それを元とする集合を定義し、これを直積集合という。このとき直積集合を
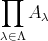 と書く。 (
と書く。 (
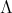 が無限集合の場合には、直積集合が空でないことを保証するために選択公理 (Zermelo’s axiom of choice) を必要とする。)
が無限集合の場合には、直積集合が空でないことを保証するために選択公理 (Zermelo’s axiom of choice) を必要とする。)
この講義では以下の記号を用いる。
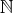 : 自然数全体の集合
: 自然数全体の集合
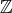 : 整数全体の集合
: 整数全体の集合
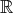 : 実数全体の集合
: 実数全体の集合
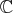 : 複素数全体の集合
: 複素数全体の集合
自然数全体の集合
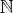 に
に
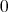 を含める場合もあるが、この講義では含めないものとする。この節では特に整数に関する基本的な性質と記号を説明する。
を含める場合もあるが、この講義では含めないものとする。この節では特に整数に関する基本的な性質と記号を説明する。
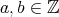 に対して、ある
に対して、ある
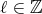 が存在して
が存在して
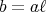 となるとき
となるとき
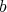 は
は
 で割り切れる、または
で割り切れる、または
 は
は
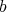 を割り切るといい
を割り切るといい
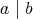 と書く。このとき、
と書く。このとき、
 は
は
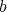 の約数 (divisor) である、
の約数 (divisor) である、
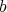 は
は
 の倍数 (multiple) である、ともいう。
の倍数 (multiple) である、ともいう。
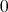 はどんな数でも割り切れ、
はどんな数でも割り切れ、
 はどんな数も割り切る。また負の数も考えることができる。
はどんな数も割り切る。また負の数も考えることができる。
有限個、または無限個の、少なくとも一つは
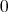 でない整数
でない整数
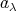 (
(
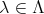 ) が与えられたとき、任意の
) が与えられたとき、任意の
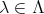 に対して
に対して
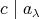 が成り立つ
が成り立つ
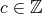 を
を
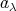 (
(
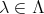 ) の公約数 (commondivisor) という。公約数のうち最大のものを最大公約数 (greatest common divisor) という。公約数は最大公約数の約数である。特に
) の公約数 (commondivisor) という。公約数のうち最大のものを最大公約数 (greatest common divisor) という。公約数は最大公約数の約数である。特に
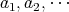 の最大公約数を
の最大公約数を
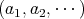 または
または
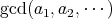 と書く。
と書く。
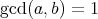 であるとき
であるとき
 と
と
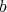 は互いに素であるという。
は互いに素であるという。
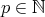 ,
,
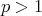 に対して
に対して
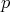 が素数 (prime number) であるとは、
が素数 (prime number) であるとは、
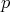 の正の約数が
の正の約数が
 と
と
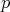 しかないこととする。これは「
しかないこととする。これは「
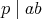 ならば、
ならば、
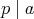 または
または
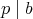 」が成り立つことと同値である。
」が成り立つことと同値である。
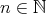 を固定する。
を固定する。
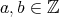 に対して
に対して
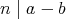 が成り立つとき
が成り立つとき
 と
と
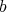 は
は
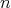 を法として合同 (congruent modulo
を法として合同 (congruent modulo
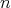 ) であるといい
) であるといい
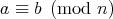 と書く。
と書く。
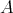 と
と
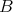 を集合とする。
を集合とする。
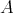 の元を一つを定めると
の元を一つを定めると
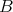 の元が一つ定まるとする。このときこの対応を写像 (map) といい
の元が一つ定まるとする。このときこの対応を写像 (map) といい
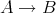 などと書く。写像に名前、例えば
などと書く。写像に名前、例えば
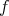 、を付けたいときには
、を付けたいときには
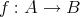 などと書く。
などと書く。
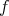 によって
によって
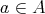 に対応する
に対応する
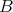 の元を
の元を
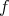 による
による
 の像といい
の像といい
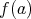 と書く。どの様な写像であるかを明記したい場合には
と書く。どの様な写像であるかを明記したい場合には

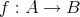 について、
について、
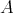 を
を
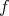 の定義域 (domain)、
の定義域 (domain)、
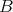 を
を
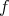 の値域 (range) という。
の値域 (range) という。
二つの写像
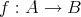 と
と
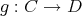 が等しいとは、
が等しいとは、
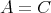 、
、
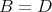 であって、任意の
であって、任意の
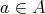 に対して
に対して
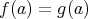 となることとする。また、このとき
となることとする。また、このとき
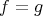 と書く。
と書く。
写像
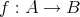 に対して
に対して
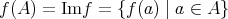
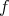 の像 (image) という。
の像 (image) という。
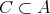 についても
についても
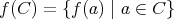 とおいて、これを
とおいて、これを
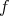 による
による
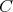 の像という。
の像という。
写像
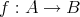 と
と
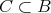 に対して
に対して
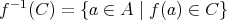
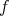 による
による
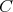 の逆像 (inverse image) という。
の逆像 (inverse image) という。
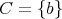 のときには
のときには
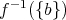 の代わりに
の代わりに
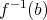 とも書く。すなわち
とも書く。すなわち
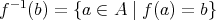
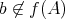 ならば明らかに
ならば明らかに
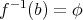 である。ここで
である。ここで
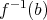 という記号を用いているが、一般にこの
という記号を用いているが、一般にこの
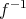 は
は
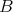 から
から
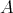 への写像ではない。
への写像ではない。
写像
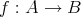 が単射 (injection) であるとは、「
が単射 (injection) であるとは、「
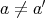 ならば
ならば
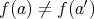 」が成り立つこととする。写像
」が成り立つこととする。写像
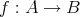 が全射 (surjection) であるとは、
が全射 (surjection) であるとは、
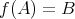 となることである。写像
となることである。写像
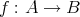 が全単射 (bijection) であるとは、
が全単射 (bijection) であるとは、
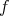 が単射、かつ全射であることである。
が単射、かつ全射であることである。
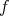 は単射である。 (
は単射である。 (
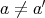 ならば
ならば
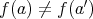 である。)
である。)
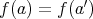 ならば
ならば
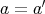 である。
である。
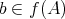 に対して
に対して
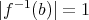 である。
である。
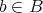 に対して
に対して
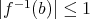 である。
である。
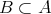 であるとき、写像
であるとき、写像
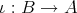 (
(
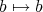 ) が定義される。これを
) が定義される。これを
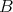 の
の
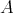 への埋め込み、または包含写像 (inclusion) という。特に
への埋め込み、または包含写像 (inclusion) という。特に
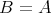 のとき、埋め込み
のとき、埋め込み
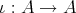 (
(
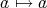 ) を
) を
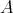 の恒等写像 (identity map) といい
の恒等写像 (identity map) といい
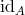 などと書く。
などと書く。
写像
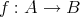 と
と
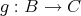 に対して、写像
に対して、写像
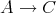 (
(
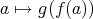 ) が定義できる。これを
) が定義できる。これを
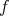 と
と
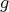 の合成写像 (composite map) といい
の合成写像 (composite map) といい
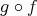 、または単に
、または単に
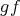 と書く。
と書く。
写像
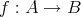 が全単射であるとき、任意の
が全単射であるとき、任意の
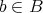 に対して
に対して
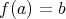 となる
となる
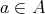 が唯一つ存在する。言い換えれば
が唯一つ存在する。言い換えれば
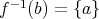 である。このとき
である。このとき
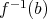 を
を
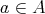 と同一視すれば、写像
と同一視すれば、写像
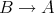 (
(
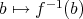 ) が得られる。これを
) が得られる。これを
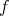 の逆写像 (inverse map) といい
の逆写像 (inverse map) といい
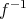 で表す。このとき、明らかに
で表す。このとき、明らかに
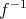 も全単射で
も全単射で
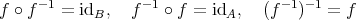
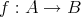 を写像とし
を写像とし
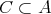 とする。このとき定義域を
とする。このとき定義域を
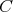 に制限して、写像
に制限して、写像
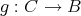 (
(
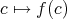 ) が得られる。これを
) が得られる。これを
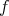 の
の
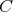 への制限 (restriction) といい
への制限 (restriction) といい
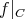 などと書く。これは、正確には、包含写像
などと書く。これは、正確には、包含写像
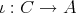 と
と
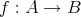 の合成写像
の合成写像
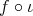 である。
である。
写像
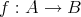 を具体的に記述するためには、任意の
を具体的に記述するためには、任意の
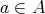 に対して
に対して
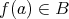 を特定すればよい。特に
を特定すればよい。特に
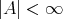 ならば、すべての
ならば、すべての
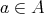 に対して
に対して
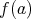 を定めればよい。例えば
を定めればよい。例えば
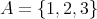 ,
,
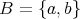 のとき
のとき
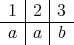
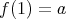 ,
,
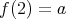 ,
,
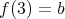 と読むことにすれば、これは写像
と読むことにすれば、これは写像
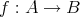 を定めている。
を定めている。
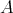 を集合とし
を集合とし
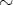 を直積集合
を直積集合
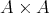 の部分集合とする。このとき
の部分集合とする。このとき
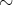 を
を
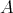 上の(二項)関係 (binary relation) という。
上の(二項)関係 (binary relation) という。
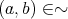 であることを
であることを
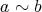 と書くことにする。
と書くことにする。
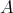 上の関係
上の関係
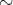 が
が
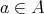 について
について
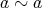 である。
である。
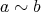 ならば
ならば
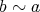 である。
である。
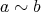 かつ
かつ
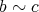 、ならば
、ならば
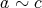 である。
である。
をすべて満たすとき、
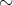 は同値律 (equivalence row) を満たすといい、
は同値律 (equivalence row) を満たすといい、
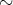 は同値関係 (equivalence relation) であるという。
は同値関係 (equivalence relation) であるという。
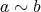 であるとき
であるとき
 と
と
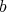 は (
は (
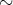 に関して) 同値であるという。
に関して) 同値であるという。
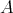 上の同値関係
上の同値関係
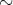 と
と
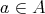 に対して
に対して
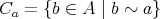
 を含む同値類 (equivalence class) という。
を含む同値類 (equivalence class) という。
同値関係
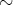 において、相異なる同値類全体の集合を
において、相異なる同値類全体の集合を
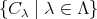 とする。このとき
とする。このとき
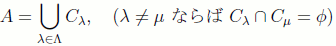
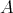 の
の
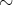 による類別という。各
による類別という。各
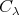 から一つずつ元
から一つずつ元
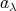 を選ぶとき、
を選ぶとき、
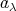 を
を
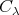 の代表元といい、
の代表元といい、
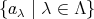 を類別
を類別
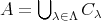 の完全代表系という。
完全代表系は代表元の選び方により変わるもので、一意的に定まるものではない。
の完全代表系という。
完全代表系は代表元の選び方により変わるもので、一意的に定まるものではない。
問1.4.2. 問
1.2.1
は
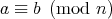 で定まる関係が
で定まる関係が
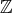 上の同値関係であることを示している。このときの類別、及び完全代表系を求めよ。
上の同値関係であることを示している。このときの類別、及び完全代表系を求めよ。
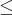 を集合
を集合
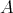 上の関係とする。
上の関係とする。
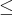 が
が
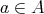 について
について
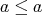 である。
である。
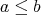 かつ
かつ
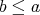 ならば
ならば
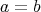 である。
である。
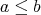 かつ
かつ
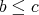 ならば
ならば
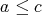 である。
である。
をすべて満たすとき
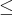 を順序 (order) といい、
を順序 (order) といい、
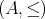 を順序集合 (ordered set) という。順序
を順序集合 (ordered set) という。順序
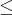 を明示しないで
を明示しないで
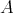 を順序集合ということもある。
を順序集合ということもある。
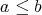 を
を
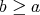 とも書く。また
とも書く。また
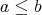 であって
であって
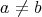 のとき、
のとき、
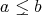 または
または
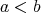 とも書く。
とも書く。
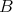 が順序集合
が順序集合
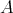 の部分集合であるとき、
の部分集合であるとき、
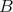 は
は
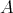 の順序によって順序集合である。
の順序によって順序集合である。
順序集合
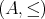 において、任意の二元
において、任意の二元
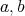 について
について
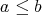 または
または
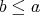 が成り立つとき、
が成り立つとき、
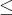 を全順序 (totally order)、
を全順序 (totally order)、
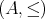 を全順序集合 (totally ordered set) という。
(単なる順序を半順序 (partially order) ともいう。)
を全順序集合 (totally ordered set) という。
(単なる順序を半順序 (partially order) ともいう。)
例1.5.2.
 を集合とし
を集合とし
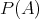 でその部分集合全体の集合を表す。
でその部分集合全体の集合を表す。
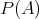 を
を
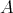 のべき集合 (power set) といい
のべき集合 (power set) といい
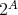 とも書く。このとき
とも書く。このとき
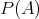 は集合の包含関係
は集合の包含関係
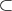 によって順序集合である。
によって順序集合である。
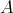 が少なくとも
が少なくとも
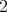 つの元を含むとき、
つの元を含むとき、
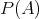 は全順序集合ではない。
は全順序集合ではない。
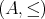 を順序集合とする。
を順序集合とする。
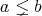 となる
となる
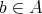 が存在しないとき、すなわち
が存在しないとき、すなわち
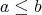 ,
,
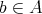 ならば
ならば
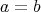 が成り立つとき、
が成り立つとき、
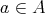 を極大元 (maximal element) という。
を極大元 (maximal element) という。
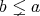 となる
となる
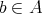 が存在しないとき、
が存在しないとき、
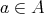 を極小元 (minimal element) という。任意の
を極小元 (minimal element) という。任意の
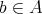 に対して
に対して
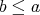 となるとき、
となるとき、
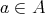 を最大元 (largest element) という。任意の
を最大元 (largest element) という。任意の
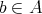 に対して
に対して
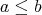 となるとき、
となるとき、
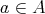 を最小元 (smallest element) という。最大 (小) 元は極大(小) 元であるが、一般に逆は正しくない。また極大 (小) 元は存在するとは限らない。
を最小元 (smallest element) という。最大 (小) 元は極大(小) 元であるが、一般に逆は正しくない。また極大 (小) 元は存在するとは限らない。
例1.5.4. 二つ以上の元を含む集合
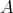 のべき集合
のべき集合
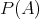 の部分集合
の部分集合
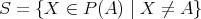 を包含関係によって順序集合と見る。このとき、任意の
を包含関係によって順序集合と見る。このとき、任意の
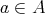 に対して
に対して
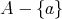 は
は
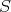 の極大元であるが最大元ではない。
の極大元であるが最大元ではない。
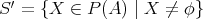 とすると、任意の
とすると、任意の
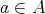 に対して
に対して
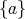 は
は
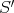 の極小元であるが最小元ではない。
の極小元であるが最小元ではない。
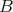 を順序集合
を順序集合
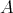 の部分集合とする。
の部分集合とする。
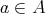 が
が
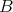 の上界であるとは、任意の
の上界であるとは、任意の
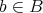 に対して
に対して
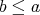 となることである。
となることである。
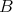 の上界が存在するとき
の上界が存在するとき
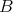 は上に有界であるという。
は上に有界であるという。
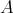 が帰納的であるとは、
が帰納的であるとは、
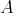 の空でない任意の全順序部分集合が上に有界であることとする。
の空でない任意の全順序部分集合が上に有界であることとする。
Zorn の補題は選択公理、整列可能定理と同値であり、厳密な数学においてはその利用に注意が必要であるが、ここでは深くは扱わないで、それを認める。
順序集合
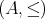 が整列集合 (well ordered set) であるとは、
が整列集合 (well ordered set) であるとは、
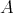 の空でない任意の部分集合に最小元が存在することである。整列可能定理は、任意の集合が適当な順序によって整列集合にできることを主張する。
の空でない任意の部分集合に最小元が存在することである。整列可能定理は、任意の集合が適当な順序によって整列集合にできることを主張する。
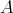 を集合とする。写像
を集合とする。写像
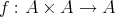 を
を
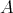 の(二項) 演算という。
の(二項) 演算という。
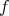 による
による
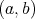 の像
の像
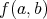 を
を
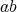 や
や
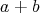 などで表す。
などで表す。
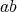 と書くとき、この演算を乗法といい
と書くとき、この演算を乗法といい
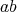 を積という。同様に、
を積という。同様に、
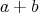 と書くとき、この演算を加法といい
と書くとき、この演算を加法といい
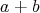 を和という。
を和という。
任意の
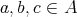 に対して
に対して
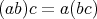 が成り立つとき、この演算は結合法則を満たすという。
が成り立つとき、この演算は結合法則を満たすという。
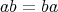 であるとき
であるとき
 と
と
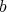 は可換であるといい、
任意の二元が可換である演算は交換法則を満たすという。一般に演算は交換法則を満たすとは限らないが、交換法則を満たさない演算に対しては加法の表記を用いない。
は可換であるといい、
任意の二元が可換である演算は交換法則を満たすという。一般に演算は交換法則を満たすとは限らないが、交換法則を満たさない演算に対しては加法の表記を用いない。
加法と乗法の両方が定義された集合
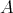 において、任意の
において、任意の
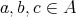 について
について
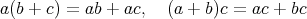
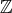 で通常の加法を演算とすれば結合法則、交換法則が成り立つ。演算を乗法にし ても同様である。また
で通常の加法を演算とすれば結合法則、交換法則が成り立つ。演算を乗法にし ても同様である。また
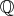 ,
,
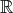 ,
,
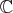 などでも加法、乗法、共に同様である。
などでも加法、乗法、共に同様である。
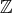 で通常の減法を演算とすれば結合法則、交換法則、共に成り立たない。
で通常の減法を演算とすれば結合法則、交換法則、共に成り立たない。
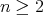 とする。実数体
とする。実数体
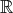 上の
上の
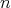 次正方行列全体の集合
次正方行列全体の集合
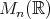 で通常の行 列の乗法を演算とすれば、結合法則は成り立つが、交換法則は成り立たない。また
で通常の行 列の乗法を演算とすれば、結合法則は成り立つが、交換法則は成り立たない。また
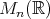 において通常の加法と乗法で分配法則が成り立つ。
において通常の加法と乗法で分配法則が成り立つ。
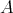 の二項演算は写像
の二項演算は写像
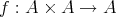 であるから、二項演算を定めるということは、任意の
であるから、二項演算を定めるということは、任意の
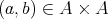 に対して
に対して
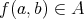 を特定することである。特に
を特定することである。特に
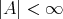 のときには、そのすべてを書き表せばよい。これには表を用いるのが効率が良い。例えば
のときには、そのすべてを書き表せばよい。これには表を用いるのが効率が良い。例えば
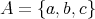 のとき
のとき
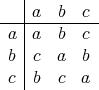
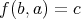 のように読むことにすれば、これは二項演算を定めている。
このような表を演算表という。演算が乗法で書かれているときには乗法表、
加法で書かれているときには加法表ともいう。
のように読むことにすれば、これは二項演算を定めている。
このような表を演算表という。演算が乗法で書かれているときには乗法表、
加法で書かれているときには加法表ともいう。
集合
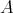 に一つの演算 (以下では乗法とする) が定義されていて、結合法則
に一つの演算 (以下では乗法とする) が定義されていて、結合法則
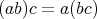 を満たすとする。このとき
を満たすとする。このとき
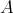 を半群 (semigroup) という。
を半群 (semigroup) という。
半群
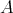 の
の
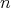 個の元
個の元
 に対して
に対して
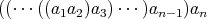 を
を
 と書く。結合法則は「
と書く。結合法則は「
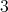 つの元の積はその順番を変えなければどの順序で演算を行っても、その結果は変わらない」ということを意味している。一般に
つの元の積はその順番を変えなければどの順序で演算を行っても、その結果は変わらない」ということを意味している。一般に
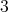 つ以上の場合でもこれは正しい。
つ以上の場合でもこれは正しい。
証明.
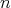 に関する帰納法で証明する。
に関する帰納法で証明する。
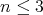 の場合は正しい。
の場合は正しい。
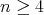 とし
とし
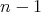 個以下の積については正しいと仮定する。最後の演算が
個以下の積については正しいと仮定する。最後の演算が
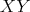 となったとし、
となったとし、
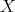 は
は
 個の元の積、
個の元の積、
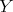 は
は
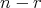 個の元の積であるとする。
個の元の積であるとする。
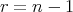 のとき、帰納法の仮定から
のとき、帰納法の仮定から
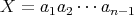 であるから
であるから
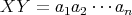 である。
である。
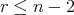 とする。帰納法の仮定から
とする。帰納法の仮定から
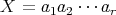 ,
,
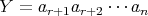 である。よって、帰納法の仮定に注意して
である。よって、帰納法の仮定に注意して
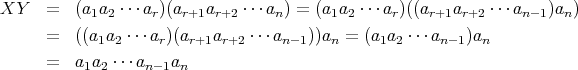

半群
 において交換法則
において交換法則
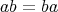 が成り立つとき、
が成り立つとき、
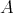 を可換半群という。可換半群においては、
を可換半群という。可換半群においては、
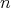 個の元の積は、元の順番、演算の順番をどの様に変えても、その結果は変わらない。
個の元の積は、元の順番、演算の順番をどの様に変えても、その結果は変わらない。
半群
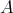 の元
の元
 で、任意の
で、任意の
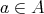 に対して
に対して
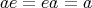 となるものが存在するとき、この
となるものが存在するとき、この
 を
を
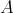 の単位元 (identity element) という。
単位元が存在する半群をモノイド (monoid)という。
の単位元 (identity element) という。
単位元が存在する半群をモノイド (monoid)という。
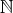 は通常の乗法で (可換) 半群である。また
は通常の乗法で (可換) 半群である。また
 が単位元になるのでモノイドであ る。
が単位元になるのでモノイドであ る。
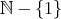 は通常の乗法で半群であるが、単位元は存在しない。
は通常の乗法で半群であるが、単位元は存在しない。
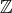 は通常の加法で (可換) 半群である。また
は通常の加法で (可換) 半群である。また
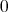 が単位元になるのでモノイドであ る。
が単位元になるのでモノイドであ る。
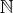 は通常の加法で半群であるが、単位元は存在しない。
は通常の加法で半群であるが、単位元は存在しない。
証明.
 ,
,
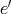 をともに単位元であるとする。
をともに単位元であるとする。
 が単位元だから
が単位元だから
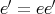 である。また
である。また
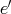 が単位元であるから
が単位元であるから
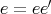 である。よって
である。よって
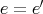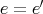 であり、単位元はただ一つである。
であり、単位元はただ一つである。

演算が乗法で書かれたモノイド
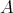 において、その単位元を
において、その単位元を
 または
または
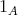 などと書く。演算が加法で書かれているときには、その単位元を
などと書く。演算が加法で書かれているときには、その単位元を
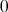 または
または
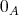 と書く。 (代数においては、多くの集合の演算を同時に考えることがあり、それぞれが単位元をもつとき、単に
と書く。 (代数においては、多くの集合の演算を同時に考えることがあり、それぞれが単位元をもつとき、単に
 と書いたのでは区別が難しい。このとき
と書いたのでは区別が難しい。このとき
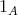 などと書き、どの半群の単位元なのかを明らかにするのである。逆に、考えている半群が一つしかないようなときには区別の必要がないので、単に
などと書き、どの半群の単位元なのかを明らかにするのである。逆に、考えている半群が一つしかないようなときには区別の必要がないので、単に
 のように表しても問題はない。)
のように表しても問題はない。)
モノイド
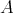 の元
の元
 と自然数
と自然数
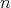 について
について
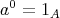 ,
,
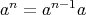 と定める。
と定める。
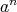 を
を
 の
の
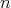 乗 (
乗 (
 to the
to the
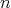 -th power) という。
-th power) という。
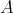 をモノイドとする。
をモノイドとする。
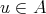 に対して
に対して
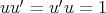 となる
となる
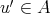 が存在するとき
が存在するとき
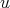 を
を
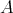 の正則元、単元、
または単数 (unit)、などという。このときの
の正則元、単元、
または単数 (unit)、などという。このときの
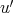 を
を
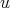 の逆元(inverse element) という。
の逆元(inverse element) という。
証明.
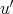 ,
,
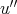 を
を
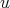 の逆元とする。このとき
の逆元とする。このとき
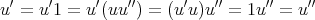

正則元
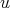 の逆元を
の逆元を
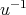 と書く。
と書く。
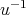 も正則元で
も正則元で
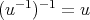 である。
である。
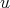 をモノイド
をモノイド
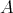 の正則元とする。
の正則元とする。
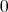 と
と
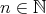 に対して
に対して
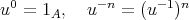
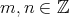 に対して成り立つ。
に対して成り立つ。
問1.7.9. モノイド
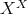 (例
1.7.5
参照) において
(例
1.7.5
参照) において
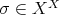 が正則元であることと、
が正則元であることと、
 が全単射であることは同値である。これを示せ。
が全単射であることは同値である。これを示せ。